Modifié le 17 Mars 2008 à 22 h 02.
Source
%@metapost: 303inequation.mp
%@Dif:3
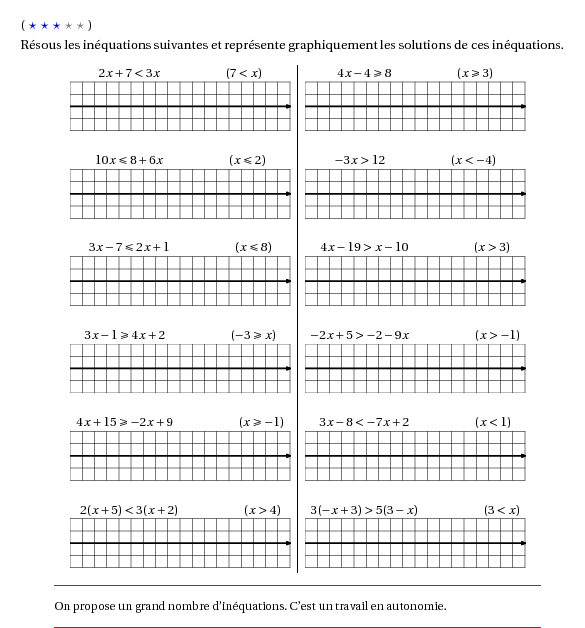
Résous les inéquations suivantes et représente graphiquement les solutions de ces inéquations.
\begin{center}
\begin{tabular}{c|c}
%\hline
$2x+7<3x$\kern20mm$(7<x)$&$4x-4\geqslant8$\kern20mm$(x\geqslant3)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
&\\
$10x\leqslant8+6x$\kern20mm$(x\leqslant2)$&$-3x>12$\kern20mm$(x<-4)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
&\\
$3x-7\leqslant2x+1$\kern20mm$(x\leqslant8)$&$4x-19>x-10$\kern20mm$(x>3)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
&\\
$3x-1\geqslant4x+2$\kern20mm$(-3\geqslant x)$&$-2x+5>-2-9x$\kern20mm$(x>-1)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
&\\
$4x+15\geqslant-2x+9$\kern20mm$(x\geqslant -1)$&$3x-8<-7x+2$\kern20mm$(x<1)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
&\\
$2(x+5)<3(x+2)$\kern20mm$(x>4)$&$3(-x+3)>5(3-x)$\kern20mm$(3<x)$\\
\includegraphics[scale=0.75]{303inequation.1}&\includegraphics[scale=0.75]{303inequation.1}\\
\end{tabular}
\end{center}
%@Commentaire: On propose un grand nombre d'inéquations. C'est un travail en autonomie.