Modifié le 26 Octobre 2006 à 19 h 33.
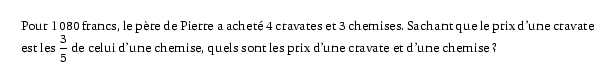
Source
%@P:exocorcp
Pour 1\,080 francs, le père de Pierre a acheté 4 cravates et 3
chemises. Sachant que le prix d'une cravate est les $\dfrac35$ de
celui d'une chemise, quels sont les prix d'une cravate et d'une
chemise ?
%@Correction:
\begin{multicols}{2}
Soit $x$ le prix d'une chemise. Alors le prix d'une cravate est $\dfrac35x$.
On a donc\par
\[\Eqalign{
1080&=3x+4\times\frac35x\cr
1080&=3x+\frac{12}5x\cr
1080&=\frac{15}5x+\frac{12}5x\cr
1080&=\frac{27}5x\cr
1080\div\frac{27}5&=x\cr
x&=1080\times\frac5{27}=200\cr
}\]
Une chemise coûte 200~F, une cravate 120~F.
\par\columnbreak\par Pour résoudre un problème :
\begin{itemize}
\item Choisir la bonne inconnue. Ici, on a le choix : le prix d'une
cravate ou le prix d'une chemise. Il est plus simple de prendre le
prix d'une chemise;
\item Poser le problème c'est à dire traduire l'énoncé sous forme
mathématique. Quel est le lien entre l'inconnue choisie et l'énoncé
? Ici, c'est le prix total de l'achat que l'on décompose : prix des
chemises plus prix des cravates;
\item Résoudre l'équation en respectant les règles de calculs;
\item Conclure correctement.
\end{itemize}
\end{multicols}