Modifié le 26 Octobre 2006 à 19 h 30.
Source
%@P:exocorcp
%@metapost:3litteralexo1.mp
%@Dif:3
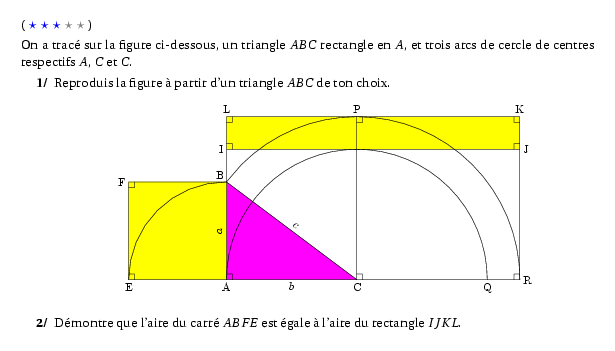
On a tracé sur la figure ci-dessous, un triangle $ABC$ rectangle en $A$, et trois arcs de cercle de centres respectifs $A$, $C$ et $C$.
\begin{myenumerate}
\item Reproduis la figure à partir d'un triangle $ABC$ de ton choix.
\[\includegraphics{3litteralexo1.1}\]
\item Démontre que l'aire du carré $ABFE$ est égale à l'aire du rectangle $IJKL$.
\end{myenumerate}
%@Correction:
Dans le triangle $ABC$, rectangle en $A$, le théorème de Pythagore permet d'écrire :
\[\Eqalign{
BC^2&=CA^2+AB^2\cr
c^2&=b^2+a^2\cr
}\]
On a
\[\Eqalign{
{\cal A}_{BFEA}&=AB^2\kern2cm&{\cal A}_{IJKL}&=IJ\times IL\cr
{\cal A}_{BFEA}&=a^2\kern2cm&{\cal A}_{IJKL}&=(c+b)\times(c-b)\cr
&&{\cal A}_{IJKL}&=c^2-b^2\cr
&&{\cal A}_{IJKL}&=a^2\cr
}\]