Modifié le 26 Octobre 2006 à 19 h 30.
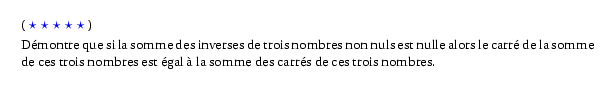
Source
%Tremplin 3eme
%@P:exocorcp
%@Dif:5
Démontre que si la somme des inverses de trois nombres non nuls est
nulle alors le carré de la somme de ces trois nombres est égal à la
somme des carrés de ces trois nombres.
%@Correction:
Soit trois nombres non nuls $x$, $y$ et $z$. On sait que $\dfrac1x+\dfrac1y+\dfrac1z=0$ ou en réduisant au même dénominateur
\[\frac{yz+xz+xy}{xyz}=0\]
Cela prouve qu'alors $yz+xz+xy=0$.
\par Donc
\[\Eqalign{
(x+y+z)^2&=(x+y)^2+2(x+y)z+z^2\cr
(x+y+z)^2&=x^2+2xy+y^2+2xz+2yz+z^2\cr
(x+y+z)^2&=x^2+y^2+z^2+2xy+2xz+2yz\cr
(x+y+z)^2&=x^2+y^2+z^2+2\underbrace{(xy+yz+zx)}_{=0}\cr
(x+y+z)^2&=x^2+y^2+z^2\cr
}\]