Modifié le 22 Octobre 2006 à 20 h 43.
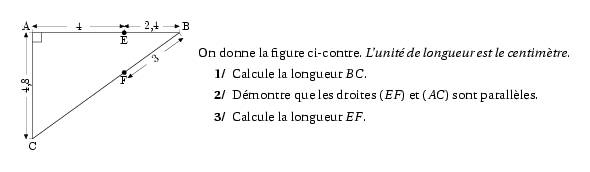
Source
%@P:exocorcp
%@metapost: 304dm03.mp
\par\compo{1}{304dm03}{1}{On donne la figure ci-contre. {\em L'unité de longueur est le centimètre.}
\begin{myenumerate}
\item Calcule la longueur $BC$.
\item Démontre que les droites $(EF)$ et $(AC)$ sont parallèles.
\item Calcule la longueur $EF$.
\end{myenumerate}
}
%@Correction:
\begin{myenumerate}
\item\pythahypo BAC{6,4}{4,8}
\item Dans le triangle $ABC$, $E$ est un point de la droite $(AB)$ et $F$ est un point de la droite $(BC)$.
\[\left.
\begin{array}{l}
\dfrac{BE}{BA}=\dfrac{2,4}{6,4}=\dfrac{24}{64}=\dfrac38\\
\\
\dfrac{BF}{BC}=\dfrac38\\
\end{array}
\right\}\frac{BE}{BA}=\frac{BF}{BC}
\]
De plus, les points $B$, $E$, $A$ sont alignés dans le même ordre que les points $B$, $F$, $C$. Donc les droites $(EF)$ et $(AC)$ sont parallèles d'après la réciproque du théorème de Thalès.
\item \Thales BACEF\ResolThales EF{4,8}38{cm}
\end{myenumerate}