Modifié le 21 Octobre 2006 à 22 h 01.
Source
%@metapost:actitrigo.mp
%@Titre: Le quart de cercle trigonométrique.
%@Dif:2
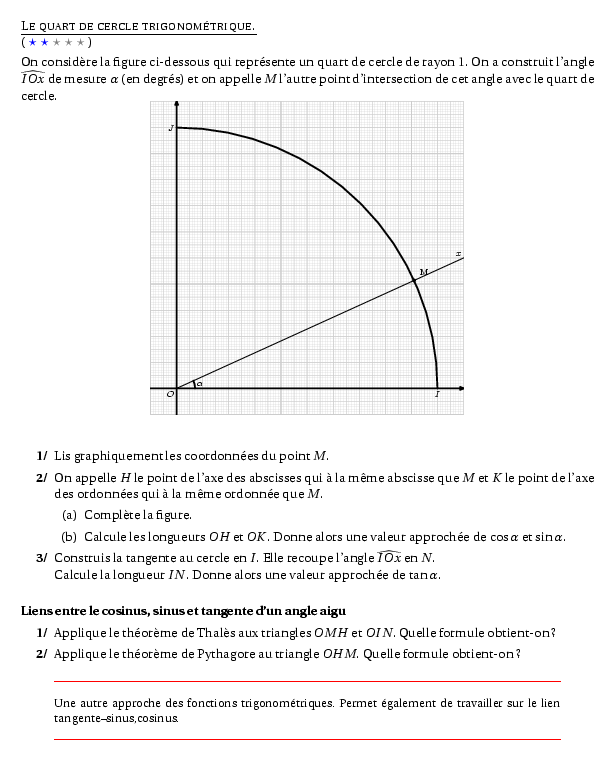
On considère la figure ci-dessous qui représente un quart de cercle de
rayon 1. On a construit l'angle $\widehat{IOx}$ de mesure $\alpha$ (en
degrés) et on appelle $M$ l'autre point d'intersection de cet angle
avec le quart de cercle.
\[\includegraphics[scale=0.8]{actitrigo.3}\]
\begin{myenumerate}
\item Lis graphiquement les coordonnées du point $M$.
\item On appelle $H$ le point de l'axe des abscisses qui à la même
abscisse que $M$ et $K$ le point de l'axe des ordonnées qui à la même
ordonnée que $M$.
\begin{enumerate}
\item Complète la figure.
\item Calcule les longueurs $OH$ et $OK$. Donne alors une valeur
approchée de $\cos\alpha$ et $\sin\alpha$.
\end{enumerate}
\item Construis la tangente au cercle en $I$. Elle recoupe l'angle
$\widehat{IOx}$ en $N$.
\\Calcule la longueur $IN$. Donne alors une valeur approchée de
$\tan\alpha$.
\end{myenumerate}
\paragraph{Liens entre le cosinus, sinus et tangente d'un angle aigu}
\begin{myenumerate}
\item Applique le théorème de Thalès aux triangles $OMH$ et
$OIN$. Quelle formule obtient-on ?
\item Applique le théorème de Pythagore au triangle $OHM$. Quelle
formule obtient-on ?
\end{myenumerate}
%@Commentaire: Une autre approche des fonctions trigonométriques. Permet également de travailler sur le lien tangente--sinus,cosinus.