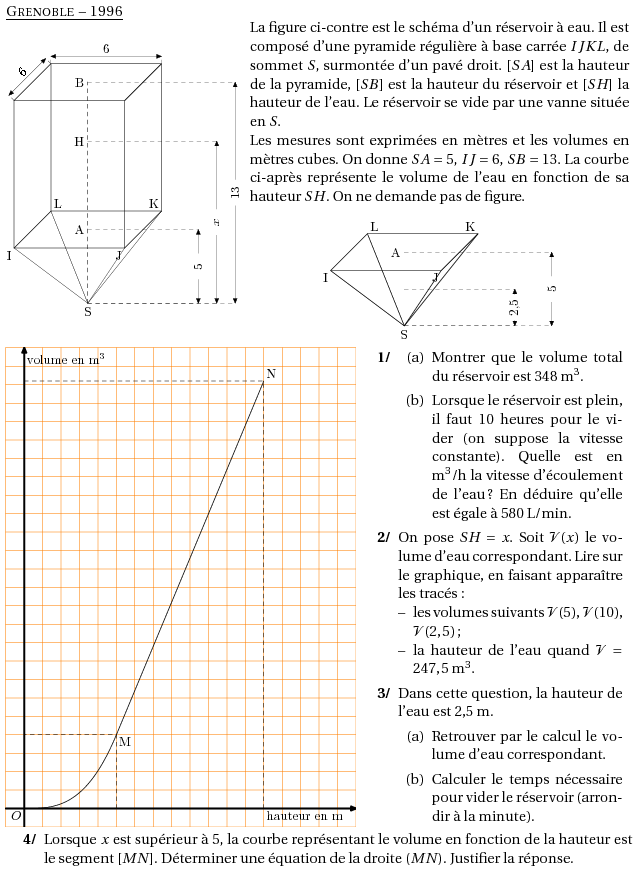
%@metapost:grenoble1996.mp %@Titre: Grenoble -- 1996 \par\compo{2}{grenoble1996}{1}{La figure ci-contre est le schéma d'un réservoir à eau. Il est composé d'une pyramide régulière à base carrée $IJKL$, de sommet $S$, surmontée d'un pavé droit. $[SA]$ est la hauteur de la pyramide, $[SB]$ est la hauteur du réservoir et $[SH]$ la hauteur de l'eau. Le réservoir se vide par une vanne située en $S$.\par Les mesures sont exprimées en mètres et les volumes en mètres cubes. On donne $SA=5$, $IJ=6$, $SB=13$. La courbe ci-après représente le volume de l'eau en fonction de sa hauteur $SH$. On ne demande pas de figure. \[\includegraphics{grenoble1996.3}\]} \par\vspace{2mm}\par \compo{1}{grenoble19961}{1}{ \begin{myenumerate} \item \begin{enumerate} \item Montrer que le volume total du réservoir est 348~m$^3$. \item Lorsque le réservoir est plein, il faut 10 heures pour le vider (on suppose la vitesse constante). Quelle est en m$^3$/h la vitesse d'écoulement de l'eau ? En déduire qu'elle est égale à 580~L/min. \end{enumerate} \item On pose $SH=x$. Soit ${\cal V}(x)$ le volume d'eau correspondant. Lire sur le graphique, en faisant apparaître les tracés : \begin{itemize} \item les volumes suivants ${\cal V}(5)$, ${\cal V}(10)$, ${\cal V}(2,5)$; \item la hauteur de l'eau quand ${\cal V}=247,5~$m$^3$. \end{itemize} \item Dans cette question, la hauteur de l'eau est 2,5~m. \begin{enumerate} \item Retrouver par le calcul le volume d'eau correspondant. \item Calculer le temps nécessaire pour vider le réservoir (arrondir à la minute). \end{enumerate} \end{myenumerate} } \begin{myenumerate} \setcounter{enumi}{3} \item Lorsque $x$ est supérieur à 5, la courbe représentant le volume en fonction de la hauteur est le segment $[MN]$. Déterminer une équation de la droite $(MN)$. Justifier la réponse. \end{myenumerate}