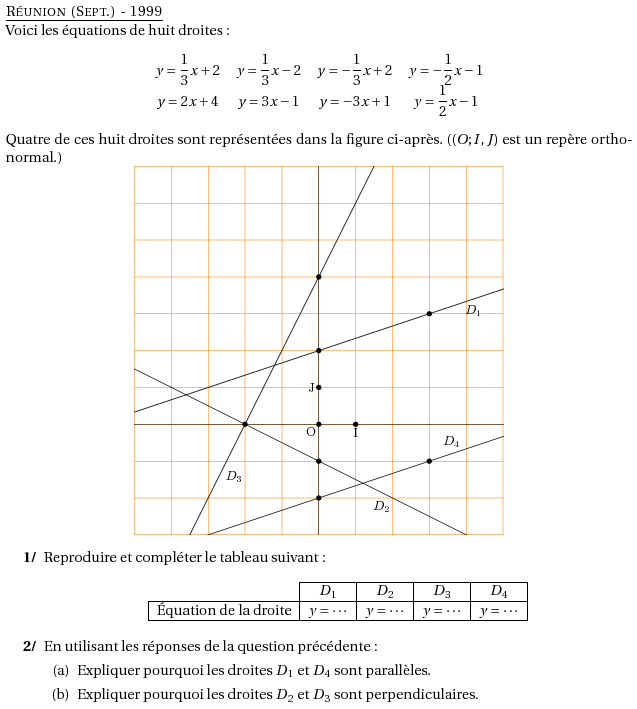
%@metapost:reunionsep1999.mp %@Titre: Réunion (Sept.) - 1999 Voici les équations de huit droites : $$ \begin{tabular}{cccc} $y=\dfrac13x+2$ & $y=\dfrac13x-2$ & $y=-\dfrac13x+2$ & $y=-\dfrac12x-1$ \\ $y=2x+4$ & $y=3x-1$ & $y=-3x+1$ & $y=\dfrac12x-1$ \\ \end{tabular} $$ Quatre de ces huit droites sont représentées dans la figure ci-après. ($(O;I,J)$ est un repère orthonormal.) $$\includegraphics{reunionsep1999.2}$$ \begin{myenumerate} \item Reproduire et compléter le tableau suivant : $$\begin{tabular}{|c|c|c|c|c|} \cline{2-5} \multicolumn{1}{c|}{}& $D_1$ & $D_2$ & $D_3$ & $D_4$ \\ \hline \'Equation de la droite & $y=\cdots$ & $y=\cdots$ & $y=\cdots$ & $y=\cdots$\\ \hline \end{tabular} $$ \item En utilisant les réponses de la question précédente : \begin{enumerate} \item Expliquer pourquoi les droites $D_1$ et $D_4$ sont parallèles. \item Expliquer pourquoi les droites $D_2$ et $D_3$ sont perpendiculaires. \end{enumerate} \end{myenumerate}