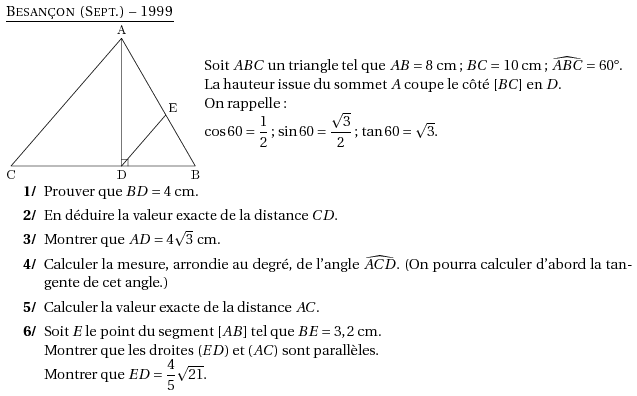
%@metapost:besanconsep1999.mp %@Titre: Besan\c con (Sept.) -- 1999 \par\compo{1}{besanconsep1999}{1}{Soit $ABC$ un triangle tel que $AB=8$~cm ; $BC=10$~cm ; $\widehat{ABC}=60$\degres. La hauteur issue du sommet $A$ coupe le côté $[BC]$ en $D$. On rappelle : $\cos 60=\dfrac12$ ; $\sin 60=\dfrac{\sqrt3}2$ ; $\tan 60=\sqrt3$. } \begin{myenumerate} \item Prouver que $BD=4$~cm. \item En déduire la valeur exacte de la distance $CD$. \item Montrer que $AD=4\sqrt3$~cm. \item Calculer la mesure, arrondie au degré, de l'angle $\widehat{ACD}$. (On pourra calculer d'abord la tangente de cet angle.) \item Calculer la valeur exacte de la distance $AC$. \item Soit $E$ le point du segment $[AB]$ tel que $BE=3,2$~cm. \\Montrer que les droites $(ED)$ et $(AC)$ sont parallèles. \\Montrer que $ED=\dfrac45\sqrt{21}$. \end{myenumerate}