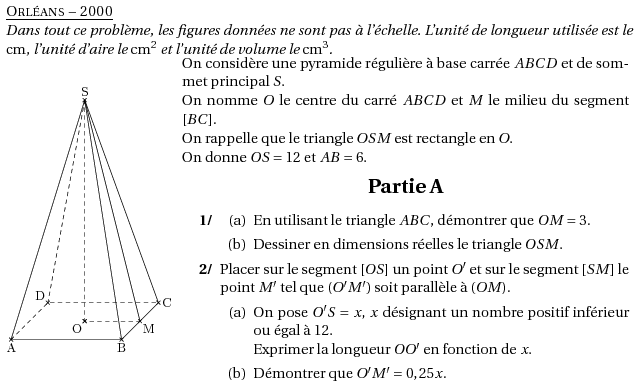
%@metapost:orleans2000.mp %@Titre: Orléans -- 2000 \textit{Dans tout ce problème, les figures données ne sont pas à l'échelle. L'unité de longueur utilisée est le {\em cm}, l'unité d'aire le {\em cm}$^2$ et l'unité de volume le {\em cm}$^3$.} \par\compo{3}{orleans2000}{1}{ On considère une pyramide régulière à base carrée $ABCD$ et de sommet principal $S$. \\On nomme $O$ le centre du carré $ABCD$ et $M$ le milieu du segment $[BC]$. \\On rappelle que le triangle $OSM$ est rectangle en $O$. \\On donne $OS=12$ et $AB=6$. \begin{center} \textbf{\Large{Partie A }} \end{center} \begin{myenumerate} \item \begin{enumerate} \item En utilisant le triangle $ABC$, démontrer que $OM=3$. \item Dessiner en dimensions réelles le triangle $OSM$. \end{enumerate} \item Placer sur le segment $[OS]$ un point $O'$ et sur le segment $[SM]$ le point $M'$ tel que $(O'M')$ soit parallèle à $(OM)$. \begin{enumerate} \item On pose $O'S=x$, $x$ désignant un nombre positif inférieur ou égal à 12. \\Exprimer la longueur $OO'$ en fonction de $x$. \item Démontrer que $O'M'=0,25x$. \end{enumerate} \end{myenumerate} }