exo25.tex

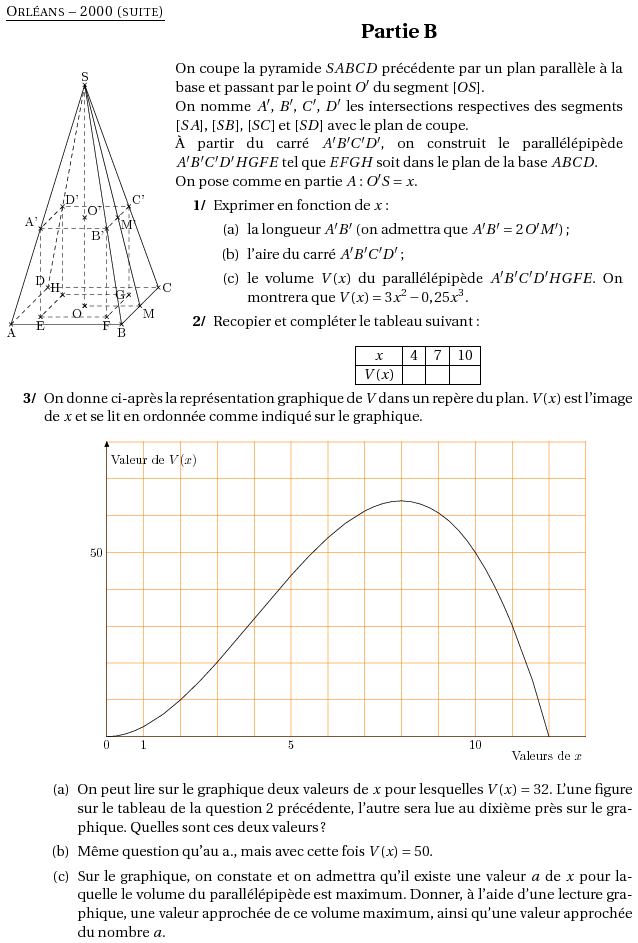
%@metapost:orleans2000.mp
%@Titre: Orléans -- 2000 (suite)
\par\compo{4}{orleans2000}{1}{
\begin{center}
\textbf{\Large{Partie B}}
\end{center}
On coupe la pyramide $SABCD$ précédente par un plan parallèle à la base et passant par le point $O'$ du segment $[OS]$.
\\On nomme $A'$, $B'$, $C'$, $D'$ les intersections respectives des segments $[SA]$, $[SB]$, $[SC]$ et $[SD]$ avec le plan de coupe.
\\\`A partir du carré $A'B'C'D'$, on construit le parallélépipède $A'B'C'D'HGFE$ tel que $EFGH$ soit dans le plan de la base $ABCD$.
\\On pose comme en partie $A$ : $O'S=x$.
\begin{myenumerate}
\item Exprimer en fonction de $x$ :
  \begin{enumerate}
  \item la longueur $A'B'$ (on admettra que $A'B'=2\,O'M'$) ;
  \item l'aire du carré $A'B'C'D'$ ;
  \item le volume $V(x)$ du parallélépipède $A'B'C'D'HGFE$. On montrera que $V(x)=3x^2-0,25x^3$.
  \end{enumerate}
\item Recopier et compléter le tableau suivant :
$$
\begin{tabular}{|c|c|c|c|}
\hline
$x$ &4&7&10 \\
\hline
$V(x)$&&& \\
\hline
\end{tabular}
$$
\end{myenumerate}
}
\begin{myenumerate}
\setcounter{enumi}{2}
\item On donne ci-après la représentation graphique de $V$ dans un repère du plan. $V(x)$ est l'image de $x$ et se lit en ordonnée comme indiqué sur le graphique.$$\includegraphics{orleans2000.5}$$
  \begin{enumerate}
  \item On peut lire sur le graphique deux valeurs de $x$ pour lesquelles $V(x)=32$. L'une figure sur le tableau de la question 2 précédente, l'autre sera lue au dixième près sur le graphique. Quelles sont ces deux valeurs ?
  \item Même question qu'au a., mais avec cette fois $V(x)=50$.
  \item Sur le graphique, on constate et on admettra qu'il existe une valeur $a$ de $x$ pour laquelle le volume du parallélépipède est maximum. Donner, à l'aide d'une lecture graphique, une valeur approchée de ce volume maximum, ainsi qu'une valeur approchée du nombre $a$.
  \end{enumerate}
\end{myenumerate}