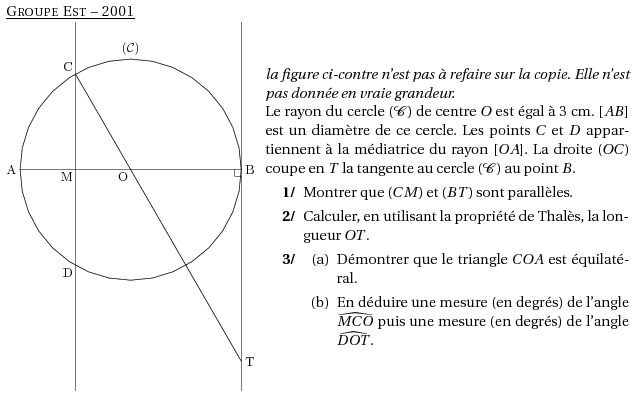
%@metapost:est2001.mp %@Titre: Groupe Est -- 2001 \par\compo{1}{est2001}{1}{ \textit{la figure ci-contre n'est pas à refaire sur la copie. Elle n'est pas donnée en vraie grandeur.} Le rayon du cercle $\cal{(C)}$ de centre $O$ est égal à 3~cm. $[AB]$ est un diamètre de ce cercle. Les points $C$ et $D$ appartiennent à la médiatrice du rayon $[OA]$. La droite $(OC)$ coupe en $T$ la tangente au cercle $\cal{(C)}$ au point $B$. \begin{myenumerate} \item Montrer que $(CM)$ et $(BT)$ sont parallèles. \item Calculer, en utilisant la propriété de Thalès, la longueur $OT$. \item \begin{enumerate} \item Démontrer que le triangle $COA$ est équilatéral. \item En déduire une mesure (en degrés) de l'angle $\widehat{MCO}$ puis une mesure (en degrés) de l'angle $\widehat{DOT}$. \end{enumerate} \end{myenumerate} }