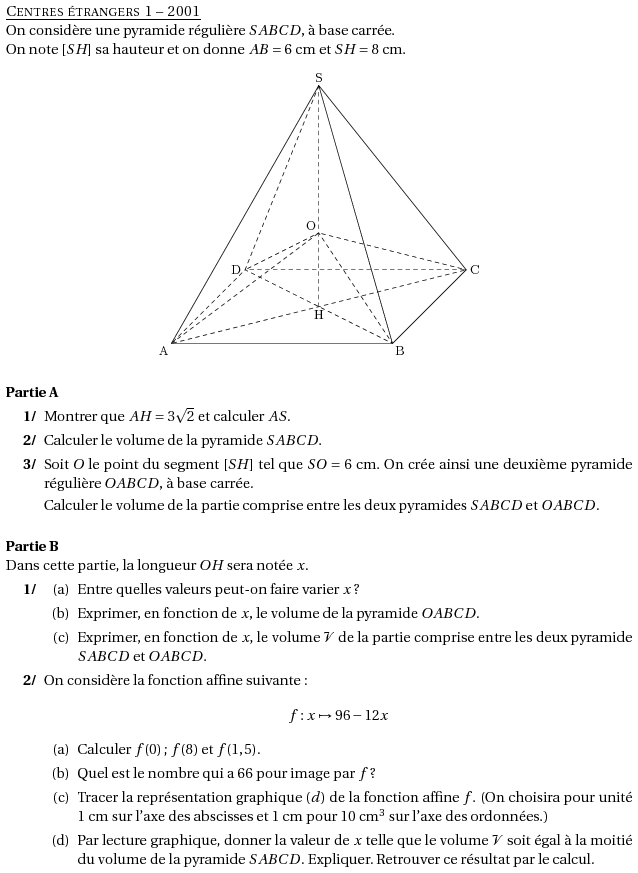
%@metapost:centresetrangers12001.mp %@Titre: Centres étrangers 1 -- 2001 On considère une pyramide régulière $SABCD$, à base carrée.\par On note $[SH]$ sa hauteur et on donne $AB=6$~cm et $SH=8$~cm. $$\includegraphics{centresetrangers12001.1}$$ \paragraph{Partie A}\subitem{} \begin{myenumerate} \item Montrer que $AH=3\sqrt2$ et calculer $AS$. \item Calculer le volume de la pyramide $SABCD$. \item Soit $O$ le point du segment $[SH]$ tel que $SO=6$~cm. On crée ainsi une deuxième pyramide régulière $OABCD$, à base carrée.\par Calculer le volume de la partie comprise entre les deux pyramides $SABCD$ et $OABCD$. \end{myenumerate} \paragraph{Partie B}\subitem{} \par Dans cette partie, la longueur $OH$ sera notée $x$. \begin{myenumerate} \item \begin{enumerate} \item Entre quelles valeurs peut-on faire varier $x$ ? \item Exprimer, en fonction de $x$, le volume de la pyramide $OABCD$. \item Exprimer, en fonction de $x$, le volume $\cal V$ de la partie comprise entre les deux pyramide $SABCD$ et $OABCD$. \end{enumerate} \item On considère la fonction affine suivante : $$f:x\mapsto96-12x$$ \begin{enumerate} \item Calculer $f(0)$; $f(8)$ et $f(1,5)$. \item Quel est le nombre qui a 66 pour image par $f$ ? \item Tracer la représentation graphique $(d)$ de la fonction affine $f$. (On choisira pour unité 1~cm sur l'axe des abscisses et 1~cm pour 10~cm$^3$ sur l'axe des ordonnées.) \item Par lecture graphique, donner la valeur de $x$ telle que le volume $\cal V$ soit égal à la moitié du volume de la pyramide $SABCD$. Expliquer. Retrouver ce résultat par le calcul. \end{enumerate} \end{myenumerate}