2003exo07.tex

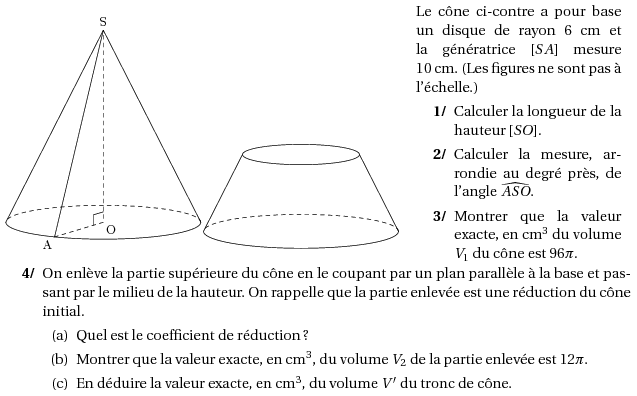
%@metapost:pondichery2003.mp
\par\dispo{1}{\includegraphics{pondichery2003.1}\includegraphics{pondichery2003.2}}{Le
  cône ci-contre a pour base un disque de rayon 6~cm et la génératrice
  $[SA]$ mesure 10~cm. (Les figures ne sont pas à l'échelle.)
  \begin{myenumerate}
    \item Calculer la longueur de la hauteur $[SO]$.
    \item Calculer la mesure, arrondie au degré près, de l'angle $\widehat{ASO}$.
    \item Montrer que la valeur exacte, en cm$^3$ du volume $V_1$ du
      cône est $96\pi$.
\end{myenumerate}
}
\begin{myenumerate}
\setcounter{enumi}{3}
    \item On enlève la partie supérieure du cône en le coupant par un
      plan parallèle à la base et passant par le milieu de la
      hauteur. On rappelle que la partie enlevée est une réduction du
      cône initial.
      \begin{enumerate}
      \item Quel est le coefficient de réduction ?
      \item Montrer que la valeur exacte, en cm$^3$, du volume $V_2$
        de la partie enlevée est $12\pi$.
      \item En déduire la valeur exacte, en cm$^3$, du volume $V'$ du
        tronc de cône.
      \end{enumerate}
  \end{myenumerate}