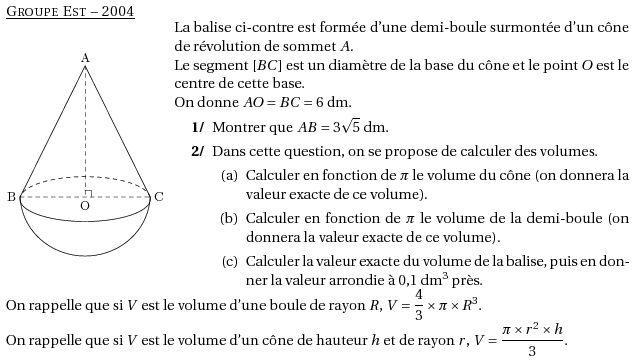
%@metapost:gpeest2004.mp %@Titre: Groupe Est -- 2004 \par\compo{2}{gpeest2004}{1}{ La balise ci-contre est formée d'une demi-boule surmontée d'un cône de révolution de sommet $A$.\\Le segment $[BC]$ est un diamètre de la base du cône et le point $O$ est le centre de cette base.\\ On donne $AO=BC=6$~dm. \begin{myenumerate} \item Montrer que $AB=3\sqrt5$~dm. \item Dans cette question, on se propose de calculer des volumes. \begin{enumerate} \item Calculer en fonction de $\pi$ le volume du cône (on donnera la valeur exacte de ce volume). \item Calculer en fonction de $\pi$ le volume de la demi-boule (on donnera la valeur exacte de ce volume). \item Calculer la valeur exacte du volume de la balise, puis en donner la valeur arrondie à 0,1~dm$^3$ près. \end{enumerate} \end{myenumerate} } \par On rappelle que si $V$ est le volume d'une boule de rayon $R$, $V=\dfrac43\times\pi\times R^3$. \par On rappelle que si $V$ est le volume d'un cône de hauteur $h$ et de rayon $r$, $V=\dfrac{\pi\times r^2\times h}3$.