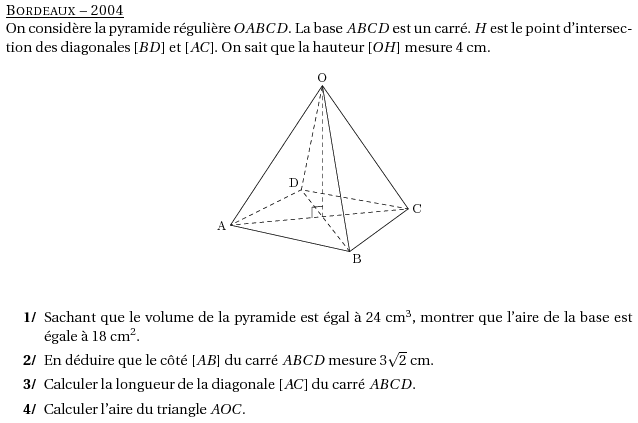
%@metapost:bordeaux2004.mp %@Titre: Bordeaux -- 2004 \par On considère la pyramide régulière $OABCD$. La base $ABCD$ est un carré. $H$ est le point d'intersection des diagonales $[BD]$ et $[AC]$. On sait que la hauteur $[OH]$ mesure 4~cm. \[\includegraphics{bordeaux2004.1}\] \begin{myenumerate} \item Sachant que le volume de la pyramide est égal à 24~cm$^3$, montrer que l'aire de la base est égale à 18~cm$^2$. \item En déduire que le côté $[AB]$ du carré $ABCD$ mesure $3\sqrt2$~cm. \item Calculer la longueur de la diagonale $[AC]$ du carré $ABCD$. \item Calculer l'aire du triangle $AOC$. \end{myenumerate}