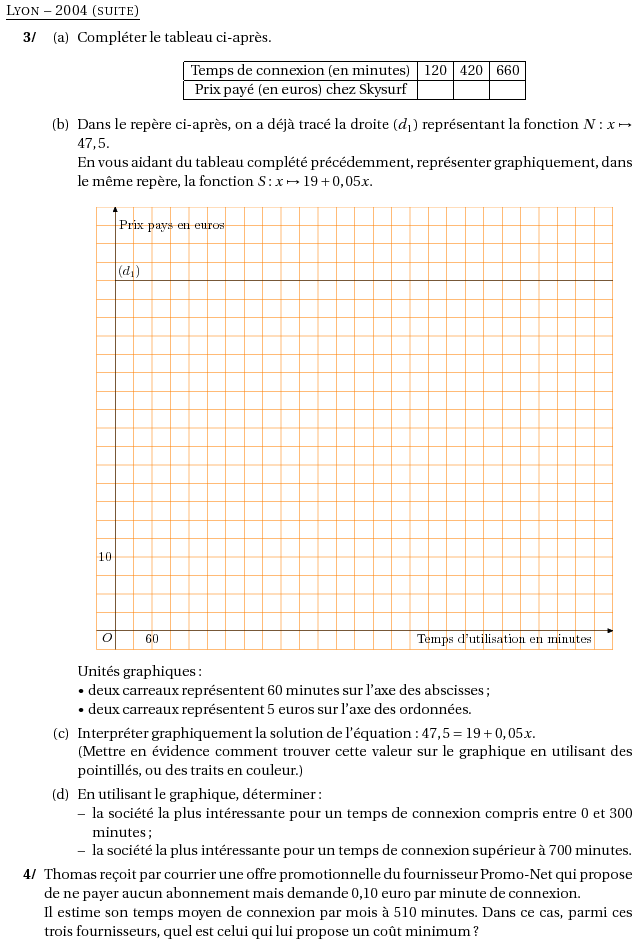
%@metapost:lyon2004.mp %@Titre: Lyon -- 2004 (suite) \begin{myenumerate} \setcounter{enumi}{2} \item \begin{enumerate} \item Compléter le tableau ci-après. \[\begin{array}{|c|c|c|c|}\hline \text{Temps de connexion (en minutes)}&120&420&660\\\hline \text{Prix payé (en euros) chez Skysurf}&&&\\\hline \end{array}\] \item Dans le repère ci-après, on a déjà tracé la droite $(d_1)$ représentant la fonction $N : x\mapsto47,5$.\\ En vous aidant du tableau complété précédemment, représenter graphiquement, dans le même repère, la fonction $S : x\mapsto 19 + 0,05x$.\\ \[\includegraphics{lyon2004.3}\] Unités graphiques :\\ $\bullet$ deux carreaux représentent 60 minutes sur l'axe des abscisses;\\ $\bullet$ deux carreaux représentent 5 euros sur l'axe des ordonnées. \item Interpréter graphiquement la solution de l'équation : $47,5=19+0,05x$.\\ (Mettre en évidence comment trouver cette valeur sur le graphique en utilisant des pointillés, ou des traits en couleur.) \item En utilisant le graphique, déterminer: \begin{itemize} \item la société la plus intéressante pour un temps de connexion compris entre 0 et 300 minutes; \item la société la plus intéressante pour un temps de connexion supérieur à 700 minutes. \end{itemize} \end{enumerate} \item Thomas re\c coit par courrier une offre promotionnelle du fournisseur Promo-Net qui propose de ne payer aucun abonnement mais demande 0,10 euro par minute de connexion.\\ Il estime son temps moyen de connexion par mois à 510 minutes. Dans ce cas, parmi ces trois fournisseurs, quel est celui qui lui propose un coût minimum ? \end{myenumerate}