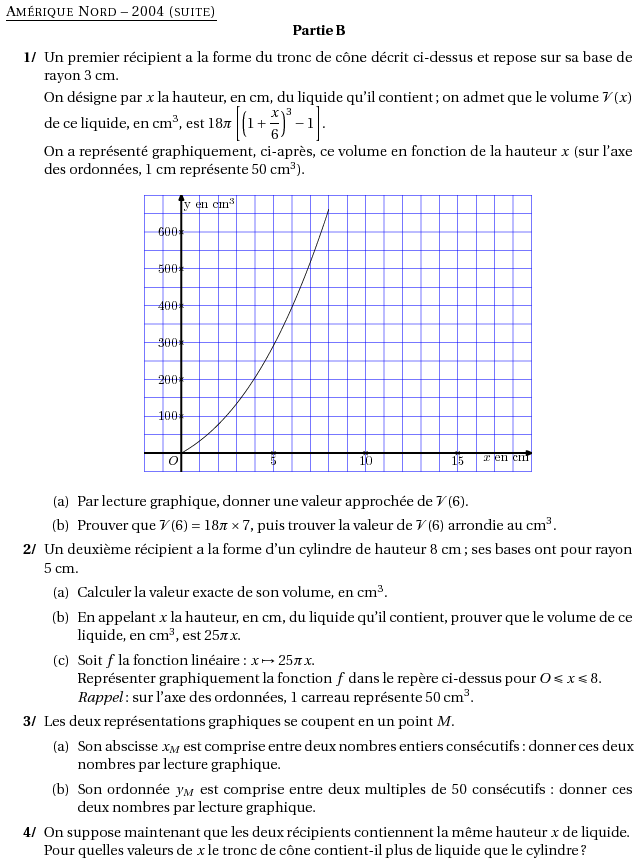
%@metapost:ameriquenord20041.mp %@Titre: Amérique Nord -- 2004 (suite) \centerline{\bf Partie B} \par %\compo{1}{ameriquenord20041}{1}{ \begin{myenumerate} \item Un premier récipient a la forme du tronc de cône décrit ci-dessus et repose sur sa base de rayon 3~cm.\par On désigne par $x$ la hauteur, en cm, du liquide qu'il contient; on admet que le volume ${\cal V}(x)$ de ce liquide, en cm$^3$, est $18\pi\left[\left(1+\dfrac{x}6\right)^3-1\right]$. \par On a représenté graphiquement, ci-après, ce volume en fonction de la hauteur $x$ (sur l'axe des ordonnées, 1~cm représente 50~cm$^3$). \[\includegraphics{ameriquenord20041.1}\] \begin{enumerate} \item Par lecture graphique, donner une valeur approchée de ${\cal V}(6)$. \item Prouver que ${\cal V}(6)=18\pi\times7$, puis trouver la valeur de ${\cal V}(6)$ arrondie au cm$^3$. \end{enumerate} %\end{myenumerate} %} %\begin{myenumerate} %\setcounter{enumi}{1} \item Un deuxième récipient a la forme d'un cylindre de hauteur 8~cm; ses bases ont pour rayon 5~cm. \begin{enumerate} \item Calculer la valeur exacte de son volume, en cm$^3$. \item En appelant $x$ la hauteur, en cm, du liquide qu'il contient, prouver que le volume de ce liquide, en cm$^3$, est $25\pi x$. \item Soit $f$ la fonction linéaire : $x\mapsto25\pi x$.\\Représenter graphiquement la fonction $f$ dans le repère ci-dessus pour $O\leqslant x\leqslant8$. \\{\em Rappel}: sur l'axe des ordonnées, 1 carreau représente 50~cm$^3$. \end{enumerate} \item Les deux représentations graphiques se coupent en un point $M$. \begin{enumerate} \item Son abscisse $x_M$ est comprise entre deux nombres entiers consécutifs : donner ces deux nombres par lecture graphique. \item Son ordonnée $y_M$ est comprise entre deux multiples de 50 consécutifs : donner ces deux nombres par lecture graphique. \end{enumerate} \item On suppose maintenant que les deux récipients contiennent la même hauteur $x$ de liquide.\\Pour quelles valeurs de $x$ le tronc de cône contient-il plus de liquide que le cylindre ? \end{myenumerate}