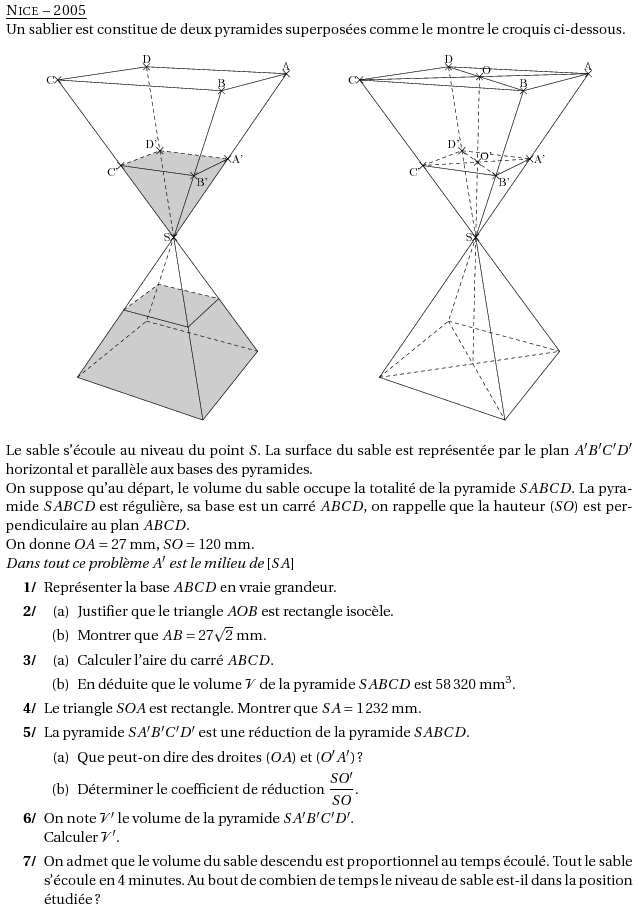
%@metapost:nice2005.mp %@Titre: Nice -- 2005 \par Un sablier est constitue de deux pyramides superposées comme le montre le croquis ci-dessous. \[\includegraphics[scale=0.9]{nice2005.4}\kern1.5cm\includegraphics[scale=0.9]{nice2005.5}\] Le sable s'écoule au niveau du point $S$. La surface du sable est représentée par le plan $A'B'C'D'$ horizontal et parallèle aux bases des pyramides. \par On suppose qu'au départ, le volume du sable occupe la totalité de la pyramide $SABCD$. La pyramide $SABCD$ est régulière, sa base est un carré $ABCD$, on rappelle que la hauteur $(SO)$ est perpendiculaire au plan $ABCD$. \par On donne $OA=27$~mm, $SO=120$~mm. \par{\em Dans tout ce problème $A'$ est le milieu de $[SA]$} \begin{myenumerate} \item Représenter la base $ABCD$ en vraie grandeur. \item \begin{enumerate} \item Justifier que le triangle $AOB$ est rectangle isocèle. \item Montrer que $AB=27\sqrt2$~mm. \end{enumerate} \item \begin{enumerate} \item Calculer l'aire du carré $ABCD$. \item En déduite que le volume $\cal V$ de la pyramide $SABCD$ est 58\,320~mm$^3$. \end{enumerate} \item Le triangle $SOA$ est rectangle. Montrer que $SA=1\,232$~mm. \item La pyramide $SA'B'C'D'$ est une réduction de la pyramide $SABCD$. \begin{enumerate} \item Que peut-on dire des droites $(OA)$ et $(O'A')$ ? \item Déterminer le coefficient de réduction $\dfrac{SO'}{SO}$. \end{enumerate} \item On note ${\cal V}'$ le volume de la pyramide $SA'B'C'D'$. \\Calculer ${\cal V}'$. \item On admet que le volume du sable descendu est proportionnel au temps écoulé. Tout le sable s'écoule en 4 minutes. Au bout de combien de temps le niveau de sable est-il dans la position étudiée ? \end{myenumerate}