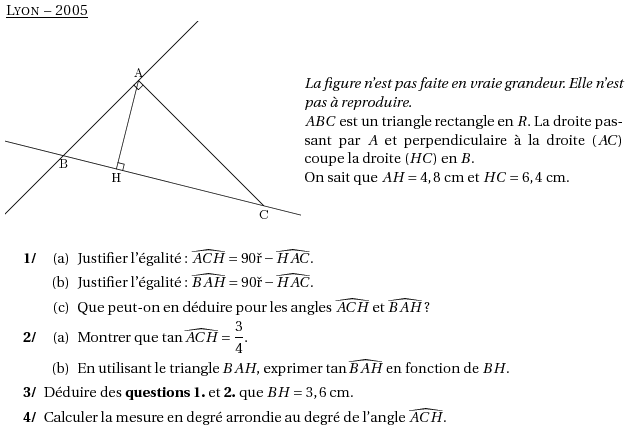
%@metapost:lyon2005.mp %@Titre: Lyon -- 2005 \par\compo{6}{lyon2005}{1}{{\em La figure n'est pas faite en vraie grandeur. Elle n'est pas à reproduire.} \par $ABC$ est un triangle rectangle en $R$. La droite passant par $A$ et perpendiculaire à la droite $(AC)$ coupe la droite $(HC)$ en $B$. \par On sait que $AH=4,8$~cm et $HC=6,4$~cm. } \begin{myenumerate} \item \begin{enumerate} \item Justifier l'égalité : $\widehat{ACH}=90\degres-\widehat{HAC}$. \item Justifier l'égalité : $\widehat{BAH}=90\degres-\widehat{HAC}$. \item Que peut-on en déduire pour les angles $\widehat{ACH}$ et $\widehat{BAH}$ ? \end{enumerate} \item \begin{enumerate} \item Montrer que $\tan\widehat{ACH}=\dfrac34$. \item En utilisant le triangle $BAH$, exprimer $\tan\widehat{BAH}$ en fonction de $BH$. \end{enumerate} \item Déduire des \textbf{questions 1.} et \textbf{2.} que $BH=3,6$~cm. \item Calculer la mesure en degré arrondie au degré de l'angle $\widehat{ACH}$. \end{myenumerate}