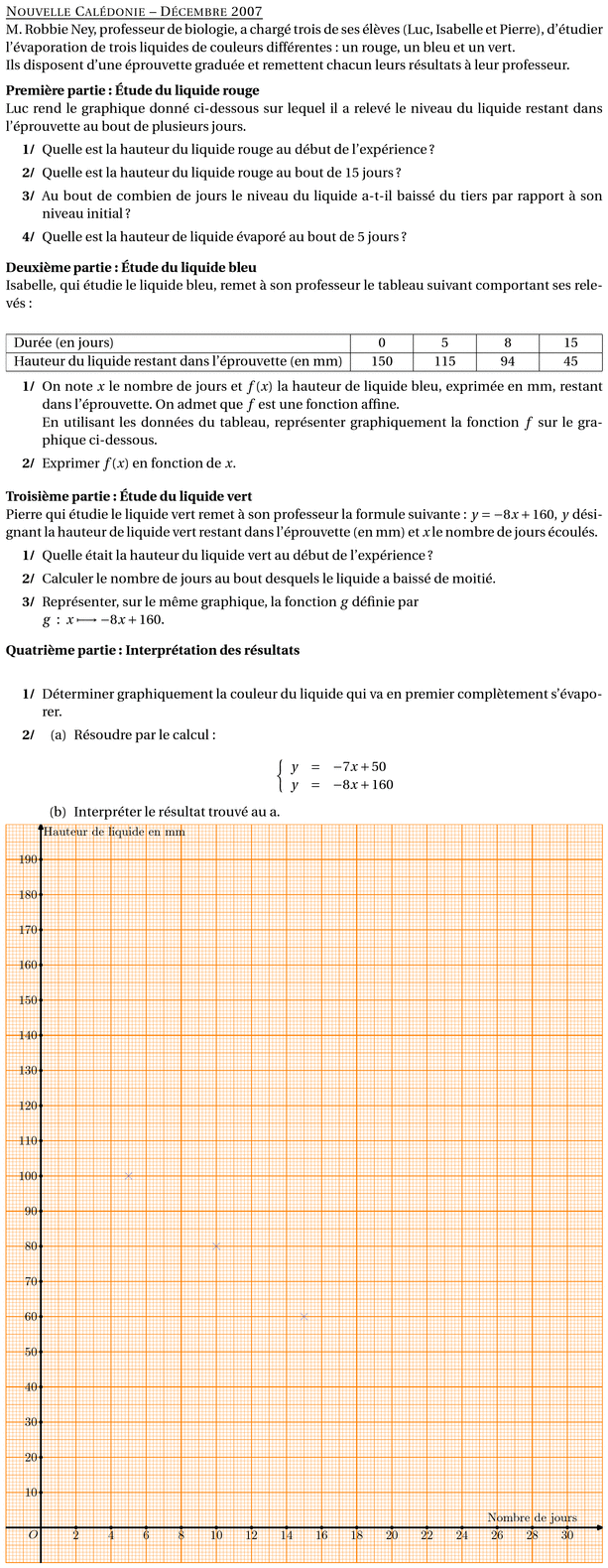
%@metapost:BNCdec2007.mp %@Titre:Nouvelle Calédonie -- Décembre 2007 M. Robbie Ney, professeur de biologie, a charg\'e trois de ses \'el\`eves (Luc, Isabelle et Pierre), d'\'etudier l'\'evaporation de trois liquides de couleurs diff\'erentes : un rouge, un bleu et un vert.\\ Ils disposent d'une \'eprouvette gradu\'ee et remettent chacun leurs r\'esultats \`a leur professeur. \medskip \noindent \textbf{Premi\`ere partie : \'Etude du liquide rouge}\\ Luc rend le graphique donn\'e ci-dessous sur lequel il a relev\'e le niveau du liquide restant dans l'\'eprouvette au bout de plusieurs jours. \begin{myenumerate} \item Quelle est la hauteur du liquide rouge au d\'ebut de l'exp\'erience ? \item Quelle est la hauteur du liquide rouge au bout de 15 jours ? \item Au bout de combien de jours le niveau du liquide a-t-il baiss\'e du tiers par rapport \`a son niveau initial ? \item Quelle est la hauteur de liquide \'evapor\'e au bout de 5~jours ? \end{myenumerate} \medskip \noindent \textbf{Deuxi\`eme partie : \'Etude du liquide bleu}\\ Isabelle, qui \'etudie le liquide bleu, remet \`a son professeur le tableau suivant comportant ses relev\'es :\\ \medskip \noindent \begin{tabularx}{\linewidth}{|l|*{4}{>{\centering \arraybackslash}X|}} \hline Dur\'ee (en jours)&0&5&8&15\\ \hline Hauteur du liquide restant dans l'\'eprouvette (en mm)&150&115&94&45\\ \hline \end{tabularx} \begin{myenumerate} \item On note $x$ le nombre de jours et $f(x)$ la hauteur de liquide bleu, exprim\'ee en mm, restant dans l'\'eprouvette. On admet que $f$ est une fonction affine.\\ En utilisant les donn\'ees du tableau, repr\'esenter graphiquement la fonction $f$ sur le graphique ci-dessous. \item Exprimer $f(x)$ en fonction de $x$. \end{myenumerate} \medskip \noindent \textbf{Troisi\`eme partie : \'Etude du liquide vert}\\ Pierre qui \'etudie le liquide vert remet \`a son professeur la formule suivante : $y = - 8 x + 160$, $y$ d\'esignant la hauteur de liquide vert restant dans l'\'eprouvette (en mm) et $x$ le nombre de jours \'ecoul\'es. \begin{myenumerate} \item Quelle \'etait la hauteur du liquide vert au d\'ebut de l'exp\'erience ? \item Calculer le nombre de jours au bout desquels le liquide a baiss\'e de moiti\'e. \item Repr\'esenter, sur le même graphique, la fonction $g$ d\'efinie par \\$g~ :~ x \longmapsto - 8 x + 160$. \end{myenumerate} \medskip \noindent \textbf{Quatri\`eme partie : Interpr\'etation des r\'esultats}\\ \begin{myenumerate} \item D\'eterminer graphiquement la couleur du liquide qui va en premier compl\`etement s'\'evaporer. \item \begin{enumerate} \item R\'esoudre par le calcul :\\ \[\left\{\begin{array}{l cl} y&=&-7x + 50\\ y&=&-8x + 160\\ \end{array}\right.\] \item Interpr\'eter le r\'esultat trouv\'e au a. \end{enumerate} \end{myenumerate} \[\includegraphics{BNCdec2007.2}\]