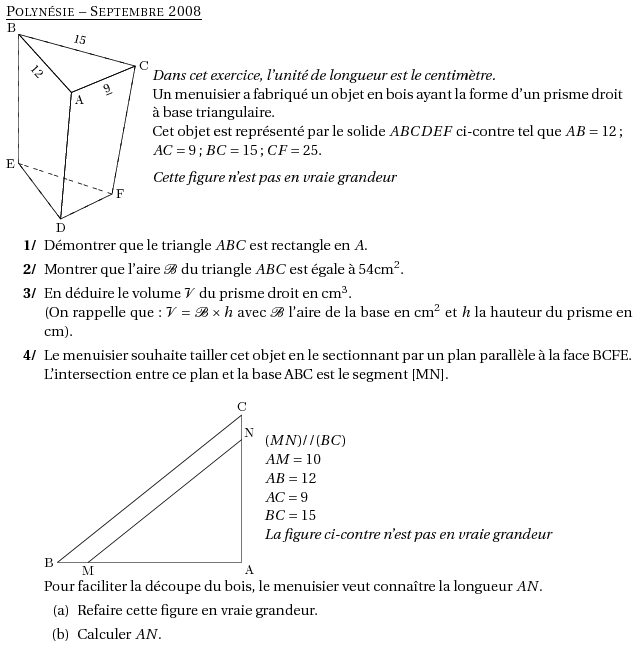
%@metapost:Polynesiesep2008.mp %@Titre:Polynésie -- Septembre 2008 \par\compo{2}{Polynesiesep2008}{1}{{\em Dans cet exercice, l'unité de longueur est le centimètre.}\\ Un menuisier a fabriqué un objet en bois ayant la forme d'un prisme droit à base triangulaire.\\ Cet objet est représenté par le solide $ABCDEF$ ci-contre tel que $AB=12$ ; $AC=9$ ; $BC=15$ ; $CF=25$. \medskip {\em Cette figure n'est pas en vraie grandeur}} \begin{myenumerate} \item Démontrer que le triangle $ABC$ est rectangle en $A$. \item Montrer que l'aire $\mathcal{B}$ du triangle $ABC$ est égale à 54cm$^2$. \item En déduire le volume $\mathcal{V}$ du prisme droit en cm$^3$.\\ (On rappelle que : $\mathcal{V} = \mathcal{B} \times h$ avec $\mathcal{B}$ l'aire de la base en cm$^2$ et $h$ la hauteur du prisme en cm). \item Le menuisier souhaite tailler cet objet en le sectionnant par un plan parallèle à la face BCFE. L'intersection entre ce plan et la base ABC est le segment [MN].\\ \par\compo{3}{Polynesiesep2008}{1}{$(MN)//(BC)$\\ $AM=10$\\ $AB=12$\\ $AC=9$\\ $BC=15$\\ \emph{La figure ci-contre n'est pas en vraie grandeur} } \par Pour faciliter la découpe du bois, le menuisier veut connaître la longueur $AN$. \begin{enumerate} \item Refaire cette figure en vraie grandeur. \item Calculer $AN$. \end{enumerate} \end{myenumerate}