exo04.tex

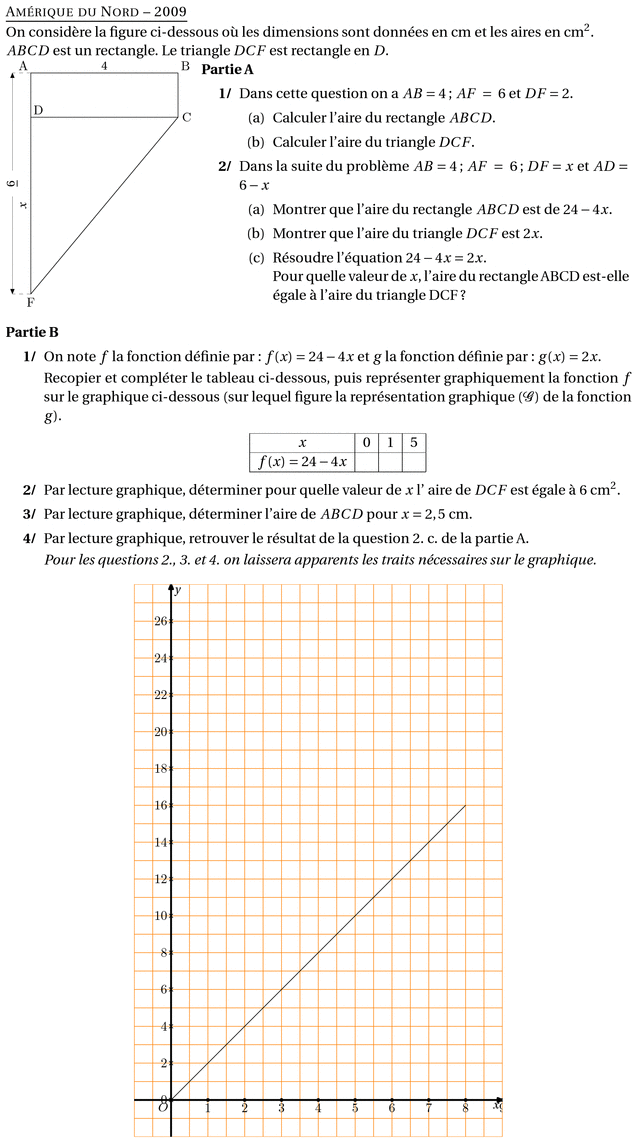
%@metapost:AMnord2009courbe.mp
%@Titre: Amérique du Nord -- 2009
On considère la figure ci-dessous où les dimensions sont données en cm
et les aires en cm$^2$.
 
$ABCD$ est un rectangle. Le triangle $DCF$ est rectangle en $D$. 
 
\par\compo{3}{AMNord2009}{1}{%
\textbf{Partie  A}
\begin{myenumerate}
\item Dans cette question on a $AB = 4$ ;  $AF~=~6$ et $DF = 2$. 
  \begin{enumerate}
  \item Calculer l'aire du rectangle $ABCD$. 
  \item Calculer l'aire du triangle $DCF$.
  \end{enumerate} 
\item Dans la suite du problème $AB = 4$ ; $AF~=~6$ ; $DF=x$ et $AD=6 - x$ 
  \begin{enumerate}
  \item Montrer que l'aire du rectangle $ABCD$ est de $24 - 4x$. 
  \item Montrer que l'aire du triangle $DCF$ est $2x$. 
  \item Résoudre l'équation $24 - 4x = 2x$. 
	\\Pour quelle valeur de $x$, l'aire du rectangle ABCD est-elle
        égale à l'aire du triangle DCF ?
\end{enumerate} 
\end{myenumerate}}
 
\vspace{0,5cm}
 
\textbf{Partie  B}
\begin{myenumerate}
\item On note $f$ la fonction définie par : $f(x) = 24 - 4x$ et $g$ la
  fonction définie par : $g(x) = 2x$.
 
Recopier et compléter le tableau ci-dessous, puis représenter graphiquement la
fonction $f$ sur le graphique ci-dessous (sur lequel figure la
représentation graphique $(\mathcal{G})$ de la fonction $g$). 
\begin{center}
  \begin{tabular}{|c|c|c|c|}
    \hline
    $x$&0&1&5\\
    \hline
    $f(x)=24-4x$&&&\\
    \hline
  \end{tabular}
\end{center}
\item Par lecture graphique, déterminer pour quelle valeur de $x$ l' aire de $DCF$ est égale à 6~cm$^2$. 
\item Par lecture graphique, déterminer l'aire de $ABCD$ pour $x = 2,5$~cm. 
\item Par lecture graphique, retrouver le résultat de la question 2. c. de la partie A. 
 
{\em Pour les questions 2.,  3. et 4. on laissera apparents les traits nécessaires sur le graphique.}
\end{myenumerate}
\[\includegraphics{AMNord2009courbe.1}\]