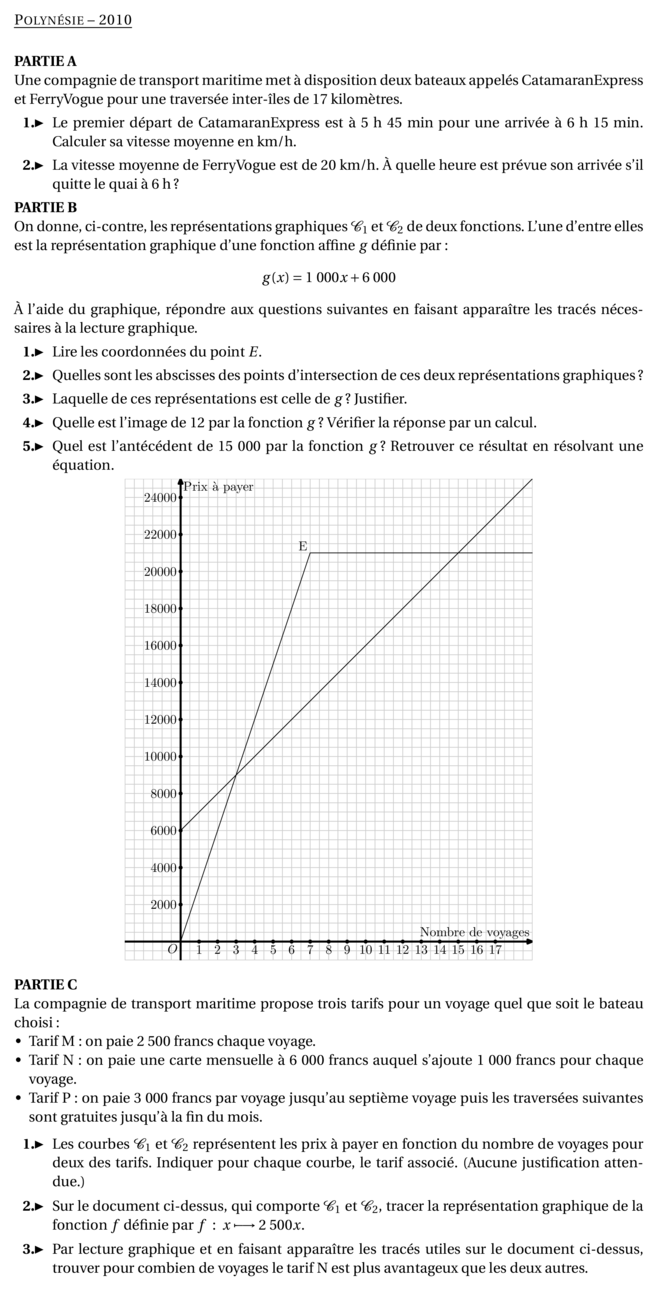
%@metapost:Polynesie2010.mp %@Titre:Polynésie -- 2010 \textbf{PARTIE A} Une compagnie de transport maritime met à disposition deux bateaux appelés CatamaranExpress et FerryVogue pour une traversée inter-îles de 17~kilomètres. \begin{Enumerate} \item Le premier départ de CatamaranExpress est à 5~h~45 min pour une arrivée à 6~h 15~min. Calculer sa vitesse moyenne en km/h. \item La vitesse moyenne de FerryVogue est de 20~km/h. \`A quelle heure est prévue son arrivée s'il quitte le quai à 6~h ? \end{Enumerate} \textbf{PARTIE B} On donne, ci-contre, les représentations graphiques $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$ de deux fonctions. L'une d'entre elles est la représentation graphique d'une fonction affine $g$ définie par : \[g(x) = \nombre{1000} x + \nombre{6000}\] \`A l'aide du graphique, répondre aux questions suivantes en faisant apparaître les tracés nécessaires à la lecture graphique. \begin{Enumerate} \item Lire les coordonnées du point $E$. \item Quelles sont les abscisses des points d'intersection de ces deux représentations graphiques ? \item Laquelle de ces représentations est celle de $g$ ? Justifier. \item Quelle est l'image de $12$ par la fonction $g$ ? Vérifier la réponse par un calcul. \item Quel est l'antécédent de \nombre{15000} par la fonction $g$ ? Retrouver ce résultat en résolvant une équation. \end{Enumerate} \[\includegraphics{Polynesie2010-3.pdf}\] \textbf{PARTIE C} La compagnie de transport maritime propose trois tarifs pour un voyage quel que soit le bateau choisi : \begin{itemize} \item[\textbullet] Tarif M : on paie \nombre{2500}~francs chaque voyage. \item[\textbullet] Tarif N : on paie une carte mensuelle à \nombre{6000}~francs auquel s'ajoute \nombre{1000}~francs pour chaque voyage. \item[\textbullet] Tarif P : on paie \nombre{3000}~francs par voyage jusqu'au septième voyage puis les traversées suivantes sont gratuites jusqu'à la fin du mois. \end{itemize} \setlength\parindent{0mm} \begin{Enumerate} \item Les courbes $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$ représentent les prix à payer en fonction du nombre de voyages pour deux des tarifs. Indiquer pour chaque courbe, le tarif associé. (Aucune justification attendue.) \item Sur le document ci-dessus, qui comporte $\mathcal{C}_{1}$ et $\mathcal{C}_{2}$, tracer la représentation graphique de la fonction $f$ définie par $f~:~x \longmapsto \nombre{2500} x.$ \item Par lecture graphique et en faisant apparaître les tracés utiles sur le document ci-dessus, trouver pour combien de voyages le tarif N est plus avantageux que les deux autres. \end{Enumerate}