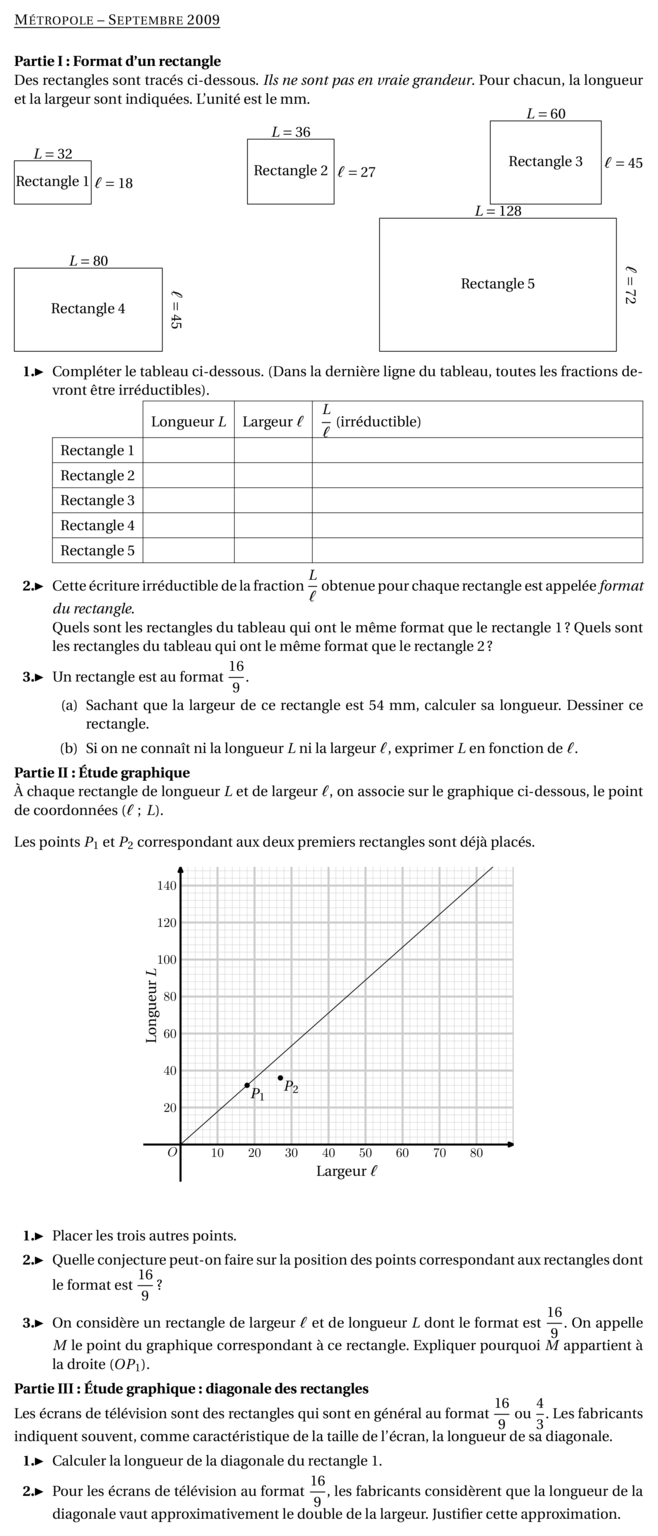
%@metapost:Metropolesep2009.mp %@Titre:Métropole -- Septembre 2009 \textbf{Partie I : Format d'un rectangle}\par Des rectangles sont tracés ci-dessous. {\em Ils ne sont pas en vraie grandeur}. Pour chacun, la longueur et la largeur sont indiquées. L'unité est le mm. \par \includegraphics{Metropolesep2009-4.pdf}\hfill \includegraphics{Metropolesep2009-5.pdf}\hfill \includegraphics{Metropolesep2009-6.pdf}\par \includegraphics{Metropolesep2009-7.pdf}\hfill \includegraphics{Metropolesep2009-8.pdf} \begin{Enumerate} \item Compléter le tableau ci-dessous. (Dans la dernière ligne du tableau, toutes les fractions devront être irréductibles). \par \renewcommand{\arraystretch}{1.3} \begin{tabularx}{\linewidth}{|l|c|c|X|} \cline{2-4} \multicolumn{1}{c|}{}&Longueur $L$&Largeur $\ell$&$\dfrac{\strut L}{\ell}$ (irréductible)\\ \hline Rectangle 1&&&\\ \hline Rectangle 2&&&\\ \hline Rectangle 3&&&\\ \hline Rectangle 4&&&\\ \hline Rectangle 5&&&\\ \hline \end{tabularx} \renewcommand{\arraystretch}{1} \item Cette écriture irréductible de la fraction $\dfrac{L}{\ell}$ obtenue pour chaque rectangle est appelée {\em format du rectangle}. \\Quels sont les rectangles du tableau qui ont le même format que le rectangle 1 ? Quels sont les rectangles du tableau qui ont le même format que le rectangle 2 ? \item Un rectangle est au format $\dfrac{16}{9}$. \begin{enumerate} \item Sachant que la largeur de ce rectangle est 54~mm, calculer sa longueur. Dessiner ce rectangle. \item Si on ne connaît ni la longueur $L$ ni la largeur $\ell$, exprimer $L$ en fonction de $\ell$. \end{enumerate} \end{Enumerate} \textbf{Partie II : Étude graphique} \par\`A chaque rectangle de longueur $L$ et de largeur $\ell$, on associe sur le graphique ci-dessous, le point de coordonnées $(\ell~;~L)$. \\Les points $P_{1}$ et $P_{2}$ correspondant aux deux premiers rectangles sont déjà placés. \[\includegraphics{Metropolesep2009-9.pdf}\] \begin{Enumerate} \item Placer les trois autres points. \item Quelle conjecture peut-on faire sur la position des points correspondant aux rectangles dont le format est $\dfrac{16}{9}$ ? \item On considère un rectangle de largeur $\ell$ et de longueur $L$ dont le format est $\dfrac{16}{9}$. On appelle $M$ le point du graphique correspondant à ce rectangle. Expliquer pourquoi $M$ appartient à la droite ($OP_{1}$). \end{Enumerate} \textbf{Partie III : Étude graphique : diagonale des rectangles} \par Les écrans de télévision sont des rectangles qui sont en général au format $\dfrac{16}{9}$ ou $\dfrac{4}{3}$. Les fabricants indiquent souvent, comme caractéristique de la taille de l'écran, la longueur de sa diagonale. \begin{Enumerate} \item Calculer la longueur de la diagonale du rectangle 1. \item Pour les écrans de télévision au format $\dfrac{16}{9}$, les fabricants considèrent que la longueur de la diagonale vaut approximativement le double de la largeur. Justifier cette approximation. \end{Enumerate}