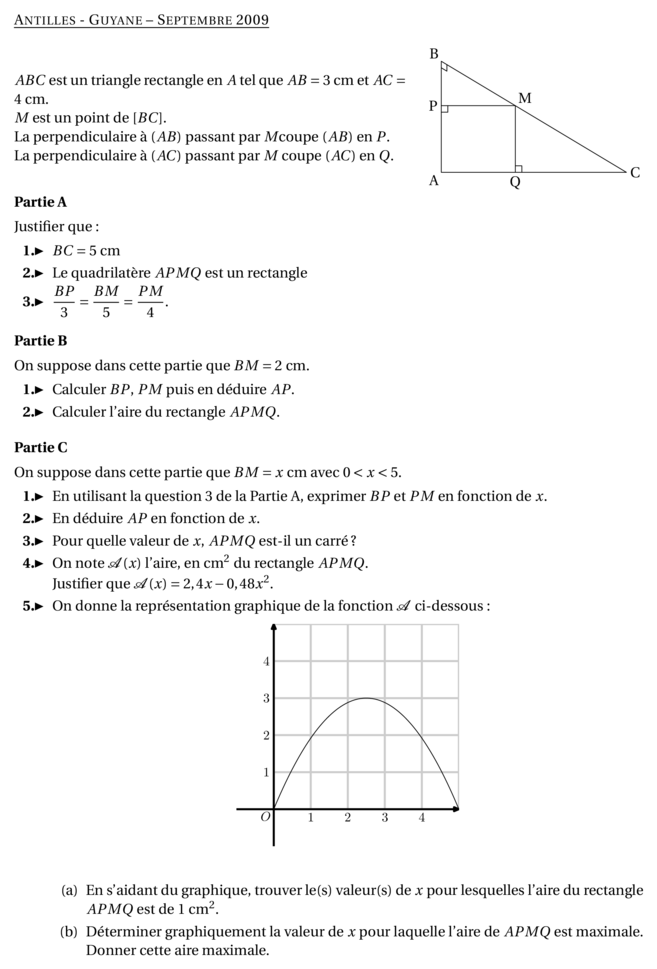
%@metapost:antillessep2009.mp %@Titre: Antilles - Guyane -- Septembre 2009 \par\compog{3}{Antillessep2009}{1}{% $ABC$ est un triangle rectangle en $A$ tel que $AB = 3$~cm et $AC = 4$~cm. $M$ est un point de $[BC]$. La perpendiculaire à $(AB)$ passant par $M $coupe $(AB)$ en $P$. La perpendiculaire à $(AC)$ passant par $M$ coupe $(AC)$ en $Q$.} \medskip \textbf{Partie A} \medskip Justifier que : \begin{Enumerate} \item $BC = 5$~cm \item Le quadrilatère $APMQ$ est un rectangle \item $\dfrac{BP}{3} = \dfrac{BM}{5} = \dfrac{PM}{4}$. \end{Enumerate} \bigskip \textbf{Partie B} \medskip On suppose dans cette partie que $BM=2$~cm. \begin{Enumerate} \item Calculer $BP$, $PM$ puis en déduire $AP$. \item Calculer l'aire du rectangle $APMQ$. \end{Enumerate} \bigskip \textbf{Partie C} \medskip On suppose dans cette partie que $BM= x$~cm avec $0 < x < 5$. \begin{Enumerate} \item En utilisant la question 3 de la Partie A, exprimer $BP$ et $PM$ en fonction de $x$. \item En déduire $AP$ en fonction de $x$. \item Pour quelle valeur de $x$, $APMQ$ est-il un carré? \item On note $\mathcal{A}(x)$ l'aire, en cm$^2$ du rectangle $APMQ$. Justifier que $\mathcal{A}(x) = 2,4x - 0,48x^2$. \item On donne la représentation graphique de la fonction $\mathcal{A}$ ci-dessous : \[\includegraphics{Antillessep2009-4.pdf}\] \begin{Enumerate} \item En s'aidant du graphique, trouver le(s) valeur(s) de $x$ pour lesquelles l'aire du rectangle $APMQ$ est de 1~cm$^2$. \item Déterminer graphiquement la valeur de $x$ pour laquelle l'aire de $APMQ$ est maximale. Donner cette aire maximale. \end{Enumerate} \end{Enumerate}