exo32.tex

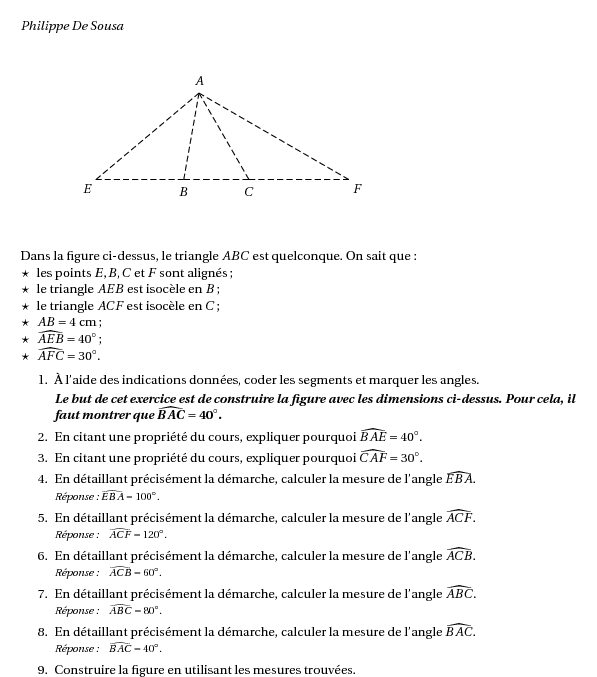
%@Auteur: Philippe De Sousa\par
\begin{center}
\begin{pspicture}(0,-1.5)(10,4)
\psset{unit=0.5cm,PointSymbol=none,linestyle=dashed}
\pstGeonode[PosAngle=-90](3,0){B}(7,0){C}%
\pstRotation[RotAngle=80,PointName=none]{B}{C}{C'}%
\pstRotation[RotAngle=-60,PointName=none]{C}{B}{B'}%
\pstInterLL[PosAngle=90]{B}{C'}{C}{B'}{A}%
\pstLineAB{A}{C}\pstLineAB{A}{B}\pstLineAB{B}{C}%
\pstRotation[RotAngle=100,PosAngle=-135]{B}{A}{E}%
\pstRotation[RotAngle=-120,PosAngle=-45]{C}{A}{F}%
\pstLineAB{A}{E}\pstLineAB{E}{B}%
\pstLineAB{A}{F}\pstLineAB{F}{C}%
\end{pspicture}
\end{center}%
Dans la figure ci-dessus, le triangle $ABC$ est quelconque. On sait
que :
\begin{itemize}
\item[$\star$] les points $E, B, C$ et $F$ sont alignés ;
\item[$\star$] le triangle $AEB$ est isocèle en $B$ ;
\item[$\star$] le triangle $ACF$ est isocèle en $C$ ;
\item[$\star$] $AB = 4$~cm ;
\item[$\star$] $\widehat{AEB} = 40^\circ$ ;
\item[$\star$] $\widehat{AFC} = 30^\circ$.
\end{itemize}
 
\begin{enumerate}
\item À l'aide des indications données, coder les segments et
marquer les angles.
 
\textbf{{\itshape Le but de cet exercice est de construire la figure
avec les dimensions ci-dessus. Pour cela, il faut montrer que
{\em $\boldsymbol{\widehat{BAC} = 40^\circ}$}.}}
 
\item En citant une propriété du cours, expliquer pourquoi $\widehat{BAE} =
40^\circ$.
 
\item En citant une propriété du cours, expliquer pourquoi $\widehat{CAF} =
30^\circ$.
 
\item En détaillant précisément la démarche, calculer la mesure de
l'angle $\widehat{EBA}$.\\{\footnotesize\itshape Réponse :
$\widehat{EBA} = 100^\circ$.}
 
\item En détaillant précisément la démarche, calculer la mesure de
l'angle $\widehat{ACF}$.\\{\footnotesize\itshape Réponse :\quad
$\widehat{ACF} = 120^\circ$.}
 
\item En détaillant précisément la démarche, calculer la mesure de
l'angle $\widehat{ACB}$.\\{\footnotesize\itshape Réponse :\quad
$\widehat{ACB} = 60^\circ$.}
 
\item En détaillant précisément la démarche, calculer la mesure de
l'angle $\widehat{ABC}$.\\{\footnotesize\itshape Réponse :\quad
$\widehat{ABC} = 80^\circ$.}
 
\item En détaillant précisément la démarche, calculer la mesure de
l'angle $\widehat{BAC}$.\\{\footnotesize\itshape Réponse :\quad
$\widehat{BAC} = 40^\circ$.}
 
\item Construire la figure en utilisant les mesures trouvées.
\end{enumerate}