exo44.tex

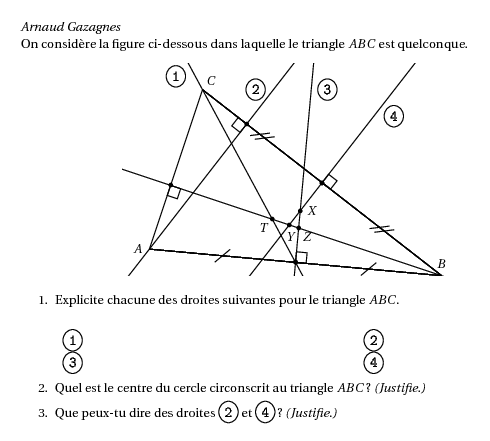
%@Auteur:Arnaud Gazagnes\par
On considère la figure ci-dessous dans laquelle le triangle $ABC$ est quelconque.
\begin{center}
{\psset{unit=0.75cm}
\begin{pspicture*}(0,0)(15,8)
\pstGeonode[PointSymbol=none,PosAngle={180,90,45}](1,1){A}(12,0){B}(3,7){C} 
\pstLineAB{A}{B}\pstLineAB{A}{C}\pstLineAB{B}{C}
\pstMiddleAB[PointName=none,PosAngle=140]{A}{B}{C'}\pstMiddleAB[PointName=none]{B}{C}{A'}
\pstSegmentMark[SegmentSymbol=MarkHash]{A}{C'} \pstSegmentMark[SegmentSymbol=MarkHash]{B}{C'} 
\pstSegmentMark[SegmentSymbol=MarkHashh]{B}{A'} \pstSegmentMark[]{C}{A'} 
{\psset{CodeFig=true,CodeFigColor=black,nodesepA=-15,nodesepB=-5,PointName=none,PointSymbolB=none,SegmentSymbol=none}\pstMediatorAB{C}{B}{A'}{M_A}
\pstMediatorAB{A}{B}{C'}{M_C}}
\pstProjection[PointName=none]{A}{C}{B}[H_B]
\pstLineAB[nodesepA=-10,nodesepB=-5]{B}{H_B}
\pstRightAngle{B}{H_B}{A}
\pstLineAB[nodesepA=-5,nodesepB=-5]{C}{C'}
\pstProjection[PointName=none]{B}{C}{A}[H_A]
\pstLineAB[nodesepA=-5,nodesepB=-5]{A}{H_A}
\pstRightAngle{A}{H_A}{C}
\pstInterLL[PosAngle=0]{C'}{M_C}{A'}{M_A}{X} 
\pstInterLL[PosAngle=280]{B}{H_B}{A'}{M_A}{Y} 
\pstInterLL[PosAngle=-45]{C'}{M_C}{B}{H_B}{Z} 
\pstInterLL[PosAngle=225]{C'}{C}{B}{H_B}{T} 
\rput(2,7.5){\psovalbox{\texttt{{\large 1}}}}
\rput(5,7){\psovalbox{\texttt{{\large 2}}}}
\rput(7.7,7){\psovalbox{\texttt{{\large 3}}}}
\rput(10.2,6){\psovalbox{\texttt{{\large 4}}}}
\end{pspicture*}}
\end{center}
\begin{enumerate}
  \item Explicite chacune des droites suivantes pour le triangle $ABC$.
 \begin{center}
\begin{tabular}{p{.475\textwidth}p{.475\textwidth}}
\psovalbox{\texttt{{\large 1}}}&\psovalbox{\texttt{{\large 2}}}\\
\psovalbox{\texttt{{\large 3}}}&\psovalbox{\texttt{{\large 4}}}\\
\end{tabular}
 \end{center}
  \item Quel est le centre du cercle circonscrit au triangle $ABC$ ? \emph{(Justifie.)}
  \item Que peux-tu dire des droites \psovalbox{\texttt{{\large 2}}} et \psovalbox{\texttt{{\large 4}}} ? \emph{(Justifie.)}
\end{enumerate}