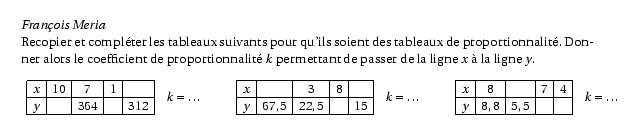
%@Auteur: François Meria\par Recopier et compléter les tableaux suivants pour qu'ils soient des tableaux de proportionnalité. Donner alors le coefficient de proportionnalité $k$ permettant de passer de la ligne $x$ à la ligne $y$. \[ \begin{array}{cc} \begin{array}{|c|c|c|c|c|} \hline x & 10 & 7 & 1 & \\ \hline y & & 364 & & 312 \\ \hline \end{array} & k=\ldots\\ \end{array} \qquad \begin{array}{cc} \begin{array}{|c|c|c|c|c|} \hline x & & 3 & 8 & \\ \hline y & 67,5 & 22,5 & & 15 \\ \hline \end{array} & k=\ldots\\ \end{array} \qquad \begin{array}{cc} \begin{array}{|c|c|c|c|c|} \hline x & 8 & & 7 & 4 \\ \hline y & 8,8 & 5,5 & & \\ \hline \end{array} & k=\ldots\\ \end{array} \]