exo64.tex

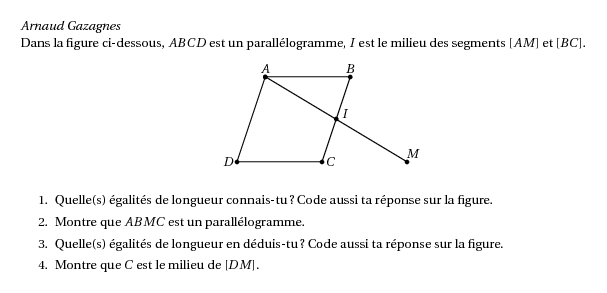
%@Auteur: Arnaud Gazagnes\par
Dans la figure ci-dessous, $ABCD$ est un parall\'elogramme, $I$ est le milieu des segments $[AM]$ et $[BC]$. 
\begin{center}
\psset{unit=0.8cm}
\begin{pspicture}(0.5,-3.5)(7.5,0.5)
\pspolygon(2,0)(5,0)(4,-3)(1,-3)(2,0)
\rput(2,.3){$A$}\rput(5,.3){$B$}\rput(4.3,-3){$C$}\rput(.7,-3){$D$}
\psline(2,0)(7,-3)
\rput(7.2,-2.7){$M$}\rput(4.8,-1.3){$I$}
\psdots(2,0)(5,0)(4,-3)(1,-3)(2,0)(7,-3)(4.5,-1.5)
\end{pspicture}
\end{center}
\begin{enumerate}
  \item Quelle(s) \'egalit\'es de longueur connais-tu? Code aussi ta r\'eponse sur la figure.
  \item Montre que $ABMC$ est un parall\'elogramme.
  \item Quelle(s) \'egalit\'es de longueur en d\'eduis-tu ? Code aussi ta r\'eponse sur la figure.
  \item Montre que $C$ est le milieu de $[DM]$.
\end{enumerate}