exo22.tex

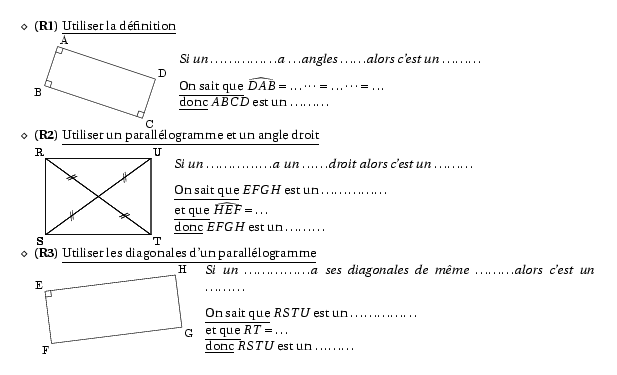
%@metapost: quadri.mp
\begin{itemize}
        \item[$\diamond$]{\bf(R1)} \underline{Utiliser la définition}\par
\compo{6}{quadri}{1}{{\em Si un \dots\dots\dots\dots\dots a \dots angles \dots\dots alors c'est un \dots\dots\dots}
\par\vskip3mm\underline{On sait que} $\widehat{DAB}=\dots\dots=\dots\dots=\dots$\par\underline{donc}
 $ABCD$ est un \dots\dots\dots
}
        \item[$\diamond$]{\bf(R2)} \underline{Utiliser un parallélogramme et un angle droit}\par
\compo{7}{quadri}{1}{
{\em Si un \dots\dots\dots\dots\dots a un \dots\dots droit alors c'est un \dots\dots\dots}
\par\vskip3mm\underline{On sait que} $EFGH$ est un \dots\dots\dots\dots\dots\par\underline{et que}
 $\widehat{HEF}=\dots$\par\underline{donc} $EFGH$ est un \dots\dots\dots
}
        \item[$\diamond$]{\bf(R3)} \underline{Utiliser les diagonales d'un parallélogramme}\par
\compo{8}{quadri}{1}{
{\em Si un \dots\dots\dots\dots\dots a ses diagonales de même \dots\dots\dots alors c'est un \dots\dots\dots}
\par\vskip3mm\underline{On sait que} $RSTU$ est un \dots\dots\dots\dots\dots\par\underline{et que}
 $RT=\dots$\par\underline{donc} $RSTU$ est un \dots\dots\dots
}
\end{itemize}