exo24.tex

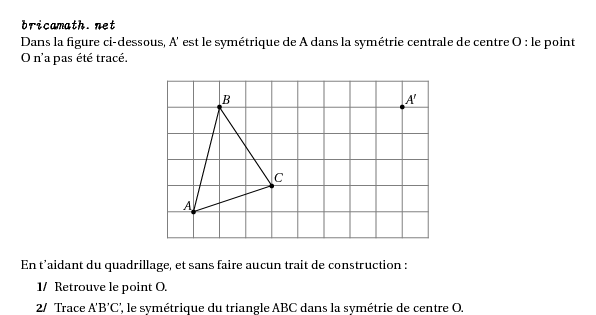
%@Auteur:\url{bricamath.net}\par
Dans la figure ci-dessous, A' est le symétrique de A dans la symétrie centrale de centre O : le point O n'a pas été tracé.\par
 
\begin{center}
	\psset{unit=0.8cm}
	\begin{pspicture}(-3,0)(7,6)
	\psgrid[subgriddiv=0,gridlabels=0,gridcolor=gray,gridwidth=0.8pt](0,0)(-3,0)(7,6)
	\psset{dotstyle=*,dotsize=4pt,linewidth=0.8pt}
	\pspolygon(-2,1)(-1,5)(1,2)
	%\pspolygon(6,5)(5,1)(3,4)% solution
	\psdots(-2,1)\rput[bl](-2.43,1.05){$A$}
	\psdots(-1,5)\rput[bl](-0.93,5.13){$B$}
	\psdots(1,2)\rput[bl](1.07,2.13){$C$}
	%\psdots(2,3)\rput[bl](2.07,3.13){$O$}% solution O
	\psdots(6,5)\rput[bl](6.07,5.13){$A'$}
	%\psdots(5,1)\rput[bl](5.07,1.13){$B'$}% solution B'
	%\psdots(3,4)\rput[bl](3.07,4.13){$C'$}% solution C'
	\end{pspicture}
\end{center}
 
En t'aidant du quadrillage, et sans faire aucun trait de construction :
\begin{myenumerate}
	\item Retrouve le point O.
	\item Trace A'B'C', le symétrique du triangle ABC dans la symétrie de centre O.
\end{myenumerate}