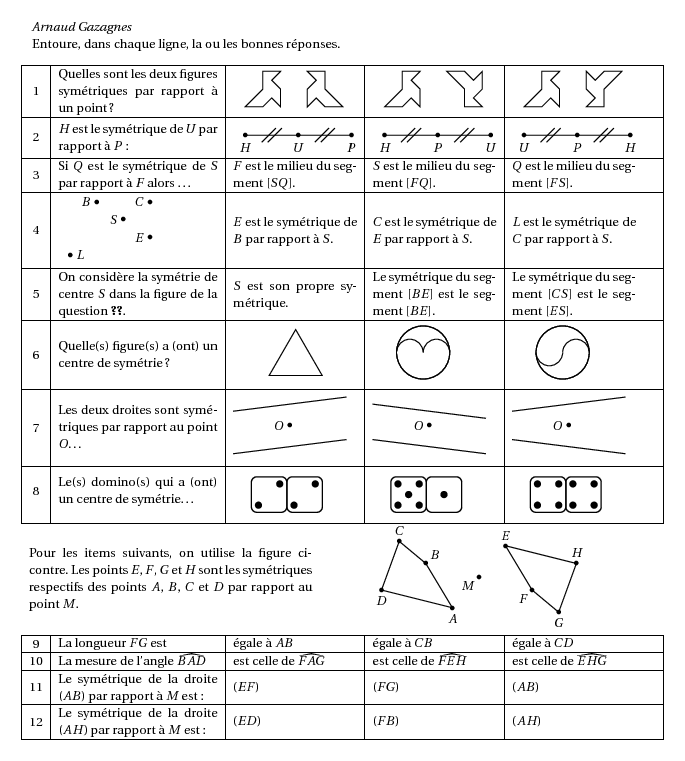
%@Auteur:Arnaud Gazagnes\par Entoure, dans chaque ligne, la ou les bonnes r\'eponses.\\ \hspace*{-0.3cm}\begin{tabular}{|c|m{4.5cm}|*{3}{m{3.5cm}|}} \hline 1&Quelles sont les deux figures sym\'etriques par rapport \`a un point ?& \quad\psset{unit=0.25cm}\begin{pspicture}(4,4)\pspolygon(0,0)(2,0)(3,1)(4,0)(4,2)(3,3)(4,4)(2,4)(2,2)\end{pspicture} \qquad \begin{pspicture}(4,4)\pspolygon(4,0)(2,0)(1,1)(0,0)(0,2)(1,3)(0,4)(2,4)(2,2)\end{pspicture}& \quad\psset{unit=0.25cm}\begin{pspicture}(4,4)\pspolygon(0,0)(2,0)(3,1)(4,0)(4,2)(3,3)(4,4)(2,4)(2,2)\end{pspicture} \qquad \begin{pspicture}(4,4)\pspolygon(0,4)(2,4)(3,3)(4,4)(4,2)(3,1)(4,0)(2,0)(2,2)\end{pspicture}& \quad\psset{unit=0.25cm}\begin{pspicture}(4,4)\pspolygon(0,0)(2,0)(3,1)(4,0)(4,2)(3,3)(4,4)(2,4)(2,2)\end{pspicture} \qquad \begin{pspicture}(4,4)\pspolygon(4,4)(2,4)(1,3)(0,4)(0,2)(1,1)(0,0)(2,0)(2,2)\end{pspicture}\\ \hline 2&$H$ est le sym\'etrique de $U$ par rapport \`a $P$ : &\quad\psset{xunit=1.5cm,yunit=0.5cm}\begin{pspicture}(-1,-1)(1,1)\psset{CodeFig=true}\pstGeonode[PosAngle={-90,-90,-90}](-1,0){H}(0,0){U}(1,0){P}\pstSegmentMark{H}{U}\pstSegmentMark{U}{P}\end{pspicture} &\quad\psset{xunit=1.5cm,yunit=0.5cm}\begin{pspicture}(-1,-1)(1,1)\psset{CodeFig=true}\pstGeonode[PosAngle={-90,-90,-90}](-1,0){H}(0,0){P}(1,0){U}\pstSegmentMark{H}{P}\pstSegmentMark{U}{P}\end{pspicture}& \quad\psset{xunit=1.5cm,yunit=0.5cm}\begin{pspicture}(-1,-1)(1,1)\psset{CodeFig=true}\pstGeonode[PosAngle={-90,-90,-90}](-1,0){U}(0,0){P}(1,0){H}\pstSegmentMark{H}{P}\pstSegmentMark{U}{P}\end{pspicture} \\ \hline 3&Si $Q$ est le sym\'etrique de $S$ par rapport \`a $F$ alors \dots&$F$ est le milieu du segment $[SQ]$.&$S$ est le milieu du segment $[FQ]$.&$Q$ est le milieu du segment $[FS]$. \\ \hline 4&\quad\psset{xunit=0.75cm,yunit=0.5cm}\begin{pspicture}(0,0.5)(4,4.5)\psdots(0,1)(3,2)(2,3)(1,4)(3,4)\uput[r](0,1){$L$}\uput[l](3,2){$E$}\uput[l](2,3){$S$}\uput[l](1,4){$B$}\uput[l](3,4){$C$}\end{pspicture}\label{qu} &$E$ est le sym\'etrique de $B$ par rapport \`a $S$.&$C$ est le sym\'etrique de $E$ par rapport \`a $S$.&$L$ est le sym\'etrique de $C$ par rapport \`a $S$.\\ \hline 5&On consid\`ere la sym\'etrie de centre $S$ dans la figure de la question \ref{qu}.&$S$ est son propre sym\'etrique.&Le sym\'etrique du segment $[BE]$ est le segment $[BE]$.& Le sym\'etrique du segment $[CS]$ est le segment $[ES]$.\\ \hline 6&Quelle(s) figure(s) a (ont) un centre de sym\'etrie ?& \quad\qquad\psset{unit=1.5cm}\begin{pspicture}(1,0.866)\SpecialCoor\pspolygon(0,0)(1,0)(1;60)\end{pspicture} &\qquad\psset{unit=0.75cm}\begin{pspicture}(-1,-1.2)(1,1.2)\pscircle(0,0){1}\psarc(0.5,0){0.5}{0}{180}\pscircle(0,0){1}\psarc(-0.5,0){0.5}{0}{180}\end{pspicture} &\qquad\psset{unit=0.75cm}\begin{pspicture}(-1,-1.2)(1,1.2)\pscircle(0,0){1}\psarc(0.5,0){0.5}{0}{180}\pscircle(0,0){1}\psarc(-0.5,0){0.5}{180}{360}\end{pspicture} \\ \hline 7&Les deux droites sont sym\'etriques par rapport au point $O$\dots& \psset{xunit=0.8cm,yunit=0.4cm}\begin{pspicture}(-2,-2.5)(2,2.5)\psdot(0,0) \uput[l](0,0){$O$}\psline(-2,1)(2,2) \psline(2,-1)(-2,-2)\end{pspicture}& \psset{xunit=0.8cm,yunit=0.4cm}\begin{pspicture}(-2,-2.5)(2,2.5)\psdot(0,0) \uput[l](0,0){$O$}\psline(-2,1.5)(2,0.5) \psline(2,-2)(-2,-1)\end{pspicture}& \psset{xunit=0.8cm,yunit=0.4cm}\begin{pspicture}(-2,-2.5)(2,2.5)\psdot(0,0) \uput[l](0,0){$O$}\psline(-2,1)(2,2) \psline(-2,-1)(2,-2)\end{pspicture} \\ \hline \rule[-8mm]{0pt}{16mm}8&Le(s) domino(s) qui a (ont) un centre de sym\'etrie\dots&\qquad\quad\psdice[unit=1cm]{2}\hspace{1cm}\psdice[unit=1cm]{2} & \qquad\quad\psdice[unit=1cm]{5}\hspace{1cm}\psdice[unit=1cm]{1}& \qquad\quad\psdice[unit=1cm]{4}\hspace{1cm}\psdice[unit=1cm]{4} \\ \hline \multicolumn{3}{m{8cm}}{Pour les items suivants, on utilise la figure ci-contre. Les points $E$, $F$, $G$ et $H$ sont les sym\'etriques respectifs des points $A$, $B$, $C$ et $D$ par rapport au point $M$.}&\multicolumn{2}{m{8cm}}{\psset{xunit=1cm,yunit=0.5cm} \begin{pspicture}(-3,-3)(3,3) \pspolygon(-0.75,-1.75)(-1.5,0.75)(-2.25,2)(-2.75,-0.75)\pspolygon(0.75,1.75)(1.5,-0.75)(2.25,-2)(2.75,0.75) \uput[d](-0.75,-1.75){$A$} \uput[ur](-1.5,0.75){$B$} \uput[u](-2.25,2){$C$} \uput[d](-2.75,-0.75){$D$} \uput[u](0.75,1.75){$E$} \uput[dl](1.5,-0.75){$F$} \uput[d](2.25,-2){$G$} \uput[u](2.75,0.75){$H$} \uput[dl](0,0){$M$} \psdots(0,0)(-0.75,-1.75)(-1.5,0.75)(-2.25,2)(-2.75,-0.75)(0.75,1.75)(1.5,-0.75)(2.25,-2)(2.75,0.75) \end{pspicture}} \\ \hline 9&La longueur $FG$ est &\'egale \`a $AB$&\'egale \`a $CB$&\'egale \`a $CD$\\ \hline 10&La mesure de l'angle $\widehat{BAD}$&est celle de $\widehat{FAG}$&est celle de $\widehat{FEH}$&est celle de $\widehat{EHG}$\\ \hline 11&Le sym\'etrique de la droite $(AB)$ par rapport \`a $M$ est :&$(EF)$&$(FG)$&$(AB)$\\ \hline 12&Le sym\'etrique de la droite $(AH)$ par rapport \`a $M$ est :&$(ED)$&$(FB)$&$(AH)$\\ \hline \end{tabular}