exo14.tex

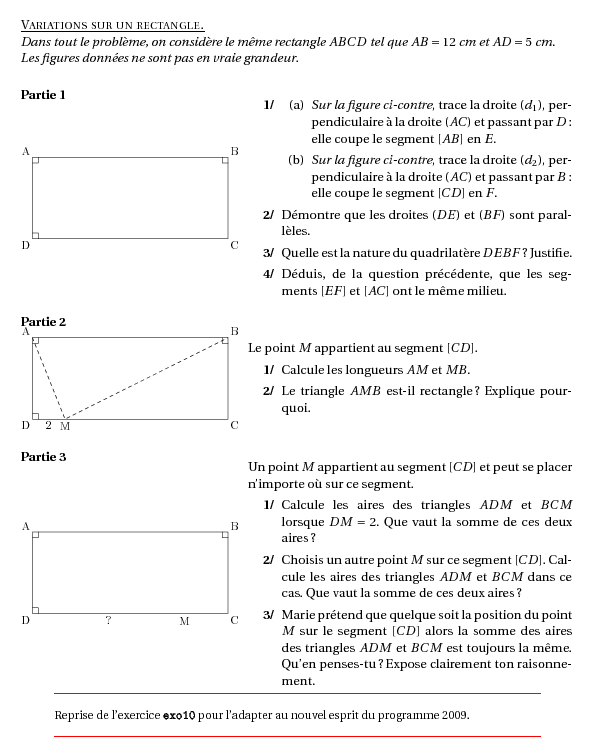
%@metapost:4diversexo14.tex
%@Titre:Variations sur un rectangle.
{\em Dans tout le problème, on considère le même rectangle $ABCD$ tel
  que $AB=12$~cm et $AD=5$~cm}.
\\{\em Les figures données ne sont pas en vraie grandeur}.
\paragraph{Partie 1}\hfill\newline
\compo{1}{4diversexo14}{1}{
  \begin{myenumerate}
    \item
      \begin{enumerate}
      \item {\em Sur la figure ci-contre}, trace la droite $(d_1)$,
        perpendiculaire à la droite $(AC)$ et passant par $D$ : elle
        coupe le segment $[AB]$ en $E$.
      \item {\em Sur la figure ci-contre}, trace la droite $(d_2)$,
        perpendiculaire à la droite $(AC)$ et passant par $B$ : elle
        coupe le segment $[CD]$ en $F$.
      \end{enumerate}
    \item Démontre que les droites $(DE)$ et $(BF)$ sont parallèles.
    \item Quelle est la nature du quadrilatère $DEBF$ ? Justifie.
    \item Déduis, de la question précédente, que les segments $[EF]$
      et $[AC]$ ont le même milieu.
  \end{myenumerate}
}
\paragraph{Partie 2}\hfill\newline
\compo{2}{4diversexo14}{1}{Le point $M$ appartient au segment $[CD]$.
  \begin{myenumerate}
    \item Calcule les longueurs $AM$ et $MB$.
    \item Le triangle $AMB$ est-il rectangle ? Explique pourquoi.
  \end{myenumerate}
}
\paragraph{Partie 3}\hfill\newline
\compo{3}{4diversexo14}{1}{Un point $M$ appartient au segment $[CD]$ et peut
  se placer n'importe où sur ce segment.
  \begin{myenumerate}
    \item Calcule les aires des triangles $ADM$ et $BCM$ lorsque
      $DM=2$. Que vaut la somme de ces deux aires ?
    \item Choisis un autre point $M$ sur ce segment $[CD]$. Calcule
      les aires des triangles $ADM$ et $BCM$ dans ce cas. Que vaut la
      somme de ces deux aires ?
    \item Marie prétend que quelque soit la position du point $M$ sur
      le segment $[CD]$ alors la somme des aires des triangles $ADM$
      et $BCM$ est toujours la même. Qu'en penses-tu ? Expose
      clairement ton raisonnement.
    \end{myenumerate}
  }
%@Commentaire:Reprise de l'exercice \verb+exo10+ pour l'adapter au nouvel esprit du programme 2009.