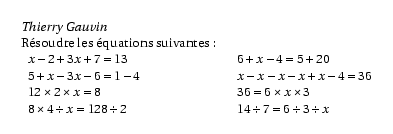
%@P:exocorcp %@Auteur: Thierry Gauvin\par Résoudre les équations suivantes : \par \begin{tabular}{p{6cm}p{6cm}} $x-2+3x+7=13$ & $6+x-4=5+20$\\ $5+x-3x-6=1-4$ & $x-x-x-x+x-4=36$\\ $12\times 2 \times x=8$ & $36=6\times x \times 3$ \\ $8\times 4 \div x=128 \div 2$ & $14\div 7=6\div 3\div x$ \\ \end{tabular} %@Correction: $x-2+3x+7=13$ ce qui donne $\,x+3x-2+7=13$ donc $4x+5=13$ c'est à dire $4x=13-5=8$ donc $x=8\div4=2$ \\ $6+x-4=5+20$ce qui donne $\,x+6-4=20+5$ donc $x+2=25$ c'est à dire $x=25-2=23$ \\ $5+x-3x-6=1-4$ ce qui donne $\,5-6+x-3x=1-4$ donc $-1-2x=-3$ soit $-1+3=2x$ soit $2=2x$ donc $x=2\div2=1$ \\ $x-x-x-x+x-4=36$ ce qui donne $\, x+x-x-x-x-4=36$ donc $2x-3x-4=36$ c'est à dire $-x-4=36$ soit $-x=36+4=40$ donc $x=-40$ \\ $12\times 2 \times x=8$ ce qui donne $\, 24 \times x=8 $ donc $x=8\div 24=\dfrac13$ donc $x=0,333$\\ $36=6\times x \times 3$ ce qui donne $\, 36=6\times 3 \times x$ donc $36=18\times x$ donc $x=36\div 18=2$\\ $8\times 4 \div x=128 \div 2$ ce qui donne $\, 32\div x=64$ donc $32 = x\times 64$ donc $x=32\div 64$ c'est à dire $x=\dfrac12$\\ $14\div 7=6\div 3\div x$ ce qui donne $\, 2=2\div x$ donc $x=2\div2=1$