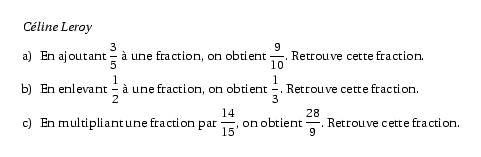
%@P:exocorcp %@Auteur: CÚline Leroy\par \begin{enumerate}[a)] \item En ajoutant $\dfrac35$ Ó une fraction, on obtient $\dfrac9{10}$. Retrouve cette fraction. \item En enlevant $\dfrac12$ Ó une fraction, on obtient $\dfrac13$. Retrouve cette fraction. \item En multipliant une fraction par $\dfrac{14}{15}$, on obtient $\dfrac{28}9$. Retrouve cette fraction. \end{enumerate} %@Correction: \begin{multicols}{3} \begin{enumerate}[a)] \item Soit $x$ la fraction que l'on cherche \begin{align*} \frac{3}{5}+x&=\frac{9}{10}\\ \frac{6}{10}+x&=\frac{9}{10}\\ \text{donc } x&=\frac{3}{10} \end{align*} \columnbreak \item Soit $y$ la fraction que l'on cherche \begin{align*} y-\frac{1}{2}&=\frac{1}{3}\\ y-\frac{3}{6}&=\frac{2}{6}\\ \text{donc } y&=\frac{5}{6} \end{align*} \columnbreak \item Soit $z$ la fraction que l'on cherche \begin{align*} z \times\frac{14}{15}&=\frac{28}{9}\\ \text{donc } z&=\frac{28}{9} \div \frac{14}{15}\\ z&=\frac{28}{9} \times \frac{15}{14}\\ z&=\frac{28\times 15}{9\times 14}\\ z&=\frac{2\times14\times3\times5}{3\times3\times14}\\ z&=\frac{10}{3} \end{align*} \end{enumerate} \end{multicols}