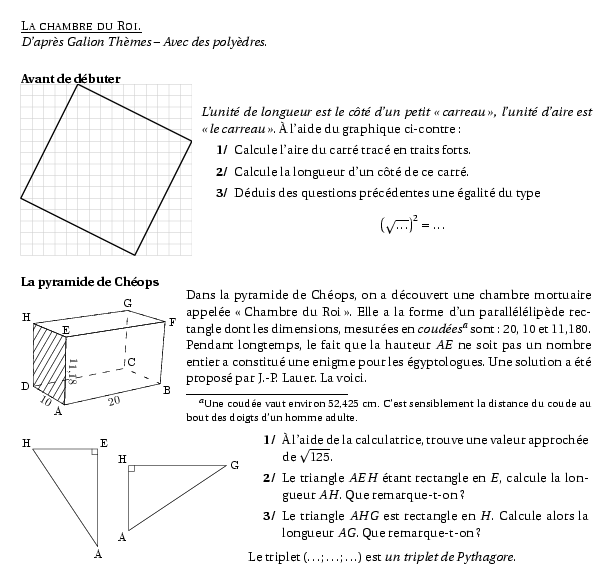
%@P:exocorcp %@metapost:4pythagoreexo60.mp %@Titre: La chambre du Roi. %@Auteur: D'après Galion Thèmes -- Avec des polyèdres.\par \paragraph{Avant de débuter}\hfill\newline \compo{1}{4pythagoreexo60}{0.7}{ {\em L'unité de longueur est le côté d'un petit \og carreau\fg, l'unité d'aire est \og le carreau\fg}. \`A l'aide du graphique ci-contre : \begin{myenumerate} \item Calcule l'aire du carré tracé en traits forts. \item Calcule la longueur d'un côté de ce carré. \item Déduis des questions précédentes une égalité du type \[\left(\sqrt{\ldots}\right)^2=\ldots\] \end{myenumerate} } \paragraph{La pyramide de Chéops}\hfill\newline \compo{2}{4pythagoreexo60}{1}{Dans la pyramide de Chéops, on a découvert une chambre mortuaire appelée \og Chambre du Roi\fg. Elle a la forme d'un parallélélipède rectangle dont les dimensions, mesurées en {\em coudées}\footnote{Une coudée vaut environ 52,425~cm. C'est sensiblement la distance du coude au bout des doigts d'un homme adulte.} sont : 20, 10 et 11,180. \par Pendant longtemps, le fait que la hauteur $AE$ ne soit pas un nombre entier a constitué une enigme pour les égyptologues. Une solution a été proposé par J.-P. Lauer. La voici. } \par\vspace{2mm}\par\compo{3}{4pythagoreexo60}{1}{\compo{4}{4pythagoreexo60}{1}{ \begin{myenumerate} \item\`A l'aide de la calculatrice, trouve une valeur approchée de $\sqrt{125}$. \item Le triangle $AEH$ étant rectangle en $E$, calcule la longueur $AH$. Que remarque-t-on ? \item Le triangle $AHG$ est rectangle en $H$. Calcule alors la longueur $AG$. Que remarque-t-on ? \end{myenumerate} Le triplet $(\ldots;\ldots;\ldots)$ est {\em un triplet de Pythagore}. }} %@Correction: \paragraph{Avant de débuter}\hfill\newline \compo{1}{4pythagoreexo60c}{0.7}{ \begin{myenumerate} \item $\mathscr{A}=15\times15-4\times\dfrac{5\times10}2=225-100=125$ \item Comme l'aire $\mathscr{A}=125$ alors le côté mesure $\sqrt{125}$. \item $\left(\sqrt{125}\right)^2=125$ \end{myenumerate} } \paragraph{La pyramide de Chéops}\hfill\newline \begin{myenumerate} \item$\sqrt{125}\approx11,18$. \item Dans le triangle $AEH$, rectangle en $E$, le théorème de Pythagore permet d'écrire : \[\Eqalign{ AH^2&=AE^2+EH^2\cr AH^2&=125+10^2\cr AH^2&=125+100\cr AH^2&=225\cr AH&=\sqrt{225}\cr AH&=15\cr }\] La longueur $AH$ mesure 15 coudées. On remarque que c'est une valeur entière. \item \pythahypo AHG{15}{20} La longueur $AG$ mesure 25 coudées. C'est encore une valeur entière. \end{myenumerate} Le triplet $(15;20;25)$ est {\em un triplet de Pythagore}.