exo40.tex

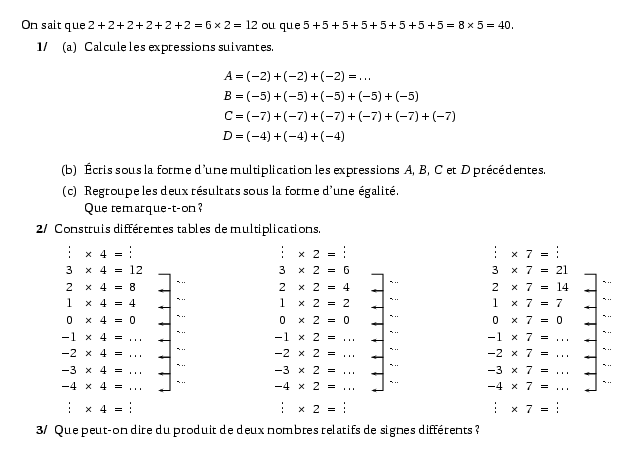
\newcommand\multablespe[1]{%
  \begin{tabular}{c!{$\times$}c!{$=$}lr}
    \vdots&#1&\vdots\\
    3&#1&\opmul*{3}{#1}{r}\opprint{r}&\rnode{A}{}\\
    2&#1&\opmul*{2}{#1}{r}\opprint{r}&\rnode{B}{}\\
    1&#1&\opmul*{1}{#1}{r}\opprint{r}&\rnode{C}{}\\
    0&#1&\opmul*{0}{#1}{r}\opprint{r}&\rnode{D}{}\\
    $-1$&#1&\ldots&\rnode{E}{}\\
    $-2$&#1&\ldots&\rnode{F}{}\\
    $-3$&#1&\ldots&\rnode{G}{}\\
    $-4$&#1&\ldots&\rnode{H}{}\\
    \vdots&#1&\vdots\\
  \end{tabular}
\ncbar{->}{A}{B}
\naput{\tiny-\ldots}
\ncbar{->}{B}{C}
\naput{\tiny-\ldots}
\ncbar{->}{C}{D}
\naput{\tiny-\ldots}
\ncbar{->}{D}{E}
\naput{\tiny-\ldots}
\ncbar{->}{E}{F}
\naput{\tiny-\ldots}
\ncbar{->}{F}{G}
\naput{\tiny-\ldots}
\ncbar{->}{G}{H}
\naput{\tiny-\ldots}
}
On sait que $2+2+2+2+2+2=6\times2=12$ ou que
$5+5+5+5+5+5+5+5=8\times5=40$.
\begin{myenumerate}
\item
\begin{enumerate}
\item Calcule les expressions suivantes.
\[\Eqalign{
A&=(-2)+(-2)+(-2)=\ldots\cr
B&=(-5)+(-5)+(-5)+(-5)+(-5)\cr
C&=(-7)+(-7)+(-7)+(-7)+(-7)+(-7)\cr
D&=(-4)+(-4)+(-4)\cr
}\]
\item \'Ecris sous la forme d'une multiplication les expressions $A$,
$B$, $C$ et $D$ précédentes.
\item Regroupe les deux résultats sous la forme d'une égalité.\\Que
remarque-t-on ?
\end{enumerate}
\item Construis différentes tables de multiplications.
\par
\multablespe{4}\hfill\multablespe{2}\hfill\multablespe{7}
\item Que peut-on dire du produit de deux nombres relatifs de signes différents ?
\end{myenumerate}