exo56.tex

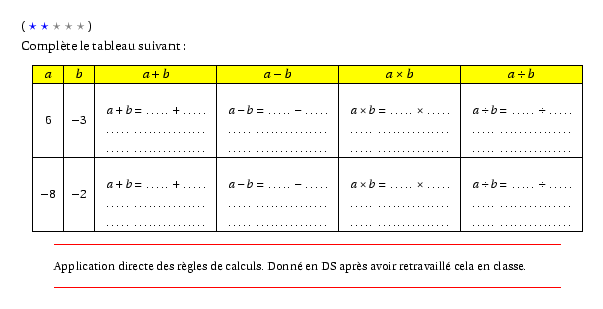
%@P:exocorcp
%@Dif:2
Complète le tableau suivant :
\renewcommand{\arrayrulewidth}{0.4mm}
\setbox1=\hbox{$a+b$}
\setbox2=\hbox{$=\hbox to8mm{\dotfill}+\hbox to8mm{\dotfill}$}
\begin{center}
\begin{tabular}{|c|c|c|c|c|c|}
\hline
\rowcolor{yellow}$a$&$b$&$a+b$&$a-b$&$a\times b$&$a\div b$\\
\hline
6&$-3$&{\small$\Eqalign{
\cr
a+b&=\hbox to8mm{\dotfill}+\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a-b&=\hbox to8mm{\dotfill}-\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a\times b&=\hbox to8mm{\dotfill}\times\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a\div b&=\hbox to8mm{\dotfill}\div\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}\\
\hline
$-8$&$-2$&{\small$\Eqalign{
\cr
a+b&=\hbox to8mm{\dotfill}+\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a-b&=\hbox to8mm{\dotfill}-\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a\times b&=\hbox to8mm{\dotfill}\times\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}&{\small$\Eqalign{
\cr
a\div b&=\hbox to8mm{\dotfill}\div\hbox to8mm{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
\hbox to\wd1{\dotfill}&\hbox to\wd2{\dotfill}\cr
}$}\\
\hline
\end{tabular}
\end{center}
%@Commentaire: Application directe des règles de calculs. Donné en DS après avoir retravaillé cela en classe.
%@Correction:
\begin{center}
\begin{tabular}{|c|c|c|c|c|c|}
\hline
\rowcolor{yellow}$a$&$b$&$a+b$&$a-b$&$a\times b$&$a\div b$\\
\hline
$-6$&3&{\small$\Eqalign{
\cr
a+b&=-6+3\cr
a+b&=-3\cr
\cr
}$}&{\small$\Eqalign{
a-b&=-6-(+3)\cr
a-b&=-6+(-3)\cr
a-b&=-9\cr
}$}&{\small$\Eqalign{
a\times b&=-6\times3\cr
a\times b&=-18\cr
}$}&{\small$\Eqalign{
a\div b&=-6\div3\cr
a\div b&=-2\cr
}$}\\
\hline
$-8$&$-2$&{\small$\Eqalign{
\cr
a+b&=-8+(-2)\cr
a+b&=-10\cr
\cr
}$}&{\small$\Eqalign{
a-b&=(-8)-(-2)\cr
a-b&=(-8)+(+2)\cr
a-b&=-6\cr
}$}&{\small$\Eqalign{
a\times b&=(-8)\times(-2)\cr
a\times b&=-16\cr
}$}&{\small$\Eqalign{
a\div b&=(-8)\div(-2)\cr
a\div b&=4\cr
}$}\\
\hline
\end{tabular}
\end{center}