exo9.tex

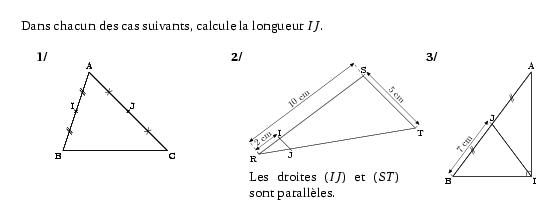
%@P:exocorcp
%@metapost:ag3td.mp
Dans chacun des cas suivants, calcule la longueur $IJ$.
\begin{multicols}{3}
\begin{myenumerate}
\item\hfill\newline\includegraphics[scale=0.8]{ag3td.5}
\par\columnbreak\par
\item\hfill\newline\includegraphics[scale=0.8]{ag3td.6}
\par Les droites $(IJ)$ et $(ST)$ sont parallèles.
\par\columnbreak\par
\item\hfill\newline\includegraphics[scale=0.8]{ag3td.7}
\end{myenumerate}
\end{multicols}
%@Correction:
\begin{myenumerate}
  \item Dans le triangle $ABC$, $I$ est le milieu du segment $[AB]$ et
    $J$ est le milieu du segment $[AC]$. Donc
    $IJ=\dfrac12BC=\dfrac12\times8,4=4,2$~cm.
  \item \Thalesf RSTIJ
\ResolThales IJ{5}{2}{10}
\item Comme le triangle $AIB$ est rectangle en $I$ alors $J$, milieu
  de $[AB]$, est le centre du cercle circonscrit au triangle
  $AIB$. Donc $IJ=I7$~cm.
\end{myenumerate}