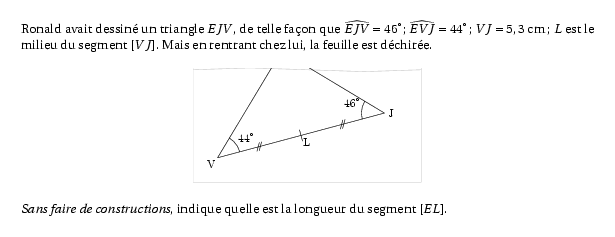
%@P:exocorcp %@metapost:trianglerectangleetcercle405exo003.mp Ronald avait dessiné un triangle $EJV$, de telle façon que $\widehat{EJV}=46$\degres; $\widehat{EVJ}=44$\degres; $VJ=5,3$~cm; $L$ est le milieu du segment $[VJ]$. Mais en rentrant chez lui, la feuille est déchirée. \[\includegraphics{trianglerectangleetcercle405exo003.1}\] {\em Sans faire de constructions}, indique quelle est la longueur du segment $[EL]$. %@Correction: Dans le triangle $EJV$, on a \[\Eqalign{ \widehat{EJV}+\widehat{JVE}+\widehat{VEJ}&=180\cr 46+44+\widehat{VEJ}&=180\cr 90+\widehat{VEJ}&=180\cr \widehat{VEJ}&=90\degres\cr }\] Comme le triangle $EJV$ est rectangle en $E$ alors $L$ est le centre du cercle circonscrit au triangle $EJV$. \par Par conséquent $LE=\dfrac12\times5,3=2,65$~cm.