exo69.tex

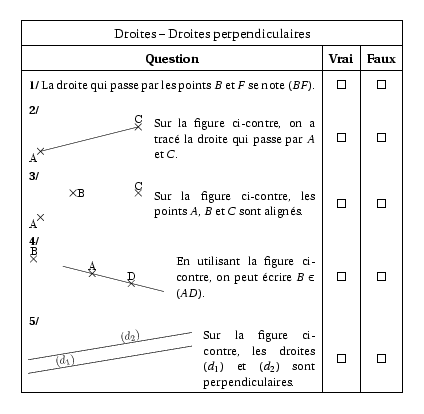
%@P:exocorcp
%@metapost:6elmtsgeoexo69.mp
\begin{center}
  \begin{VF}{Droites -- Droites perpendiculaires}
    La droite qui passe par les points $B$ et $F$ se note
    $(BF)$.&\vr&\fa\\
    \hfill\newline\compo{1}{6elmtsgeoexo69}{1}{Sur la figure ci-contre, on a
      tracé la droite qui passe par $A$
    et $C$.}&\fa&\vr\\
  \hfill\newline\compo{2}{6elmtsgeoexo69}{1}{Sur la figure ci-contre, les points $A$, $B$ et
    $C$ sont alignés.}&\fa&\vr\\
  \hfill\newline\compo{3}{6elmtsgeoexo69}{1}{En utilisant la figure
    ci-contre, on peut écrire $B\in(AD)$.}&\vr&\fa\\
  \hfill\newline\compo{4}{6elmtsgeoexo69}{1}{Sur la figure ci-contre,
    les droites $(d_1)$ et $(d_2)$ sont perpendiculaires.}&\fa&\vr\\
  \end{VF}
\end{center}
%@Correction:
\begin{center}
  \begin{VFcor}{Droites -- Droites perpendiculaires}
    La droite qui passe par les points $B$ et $F$ se note
    $(BF)$.&\vr&\fa\\
    \hfill\newline\compo{1}{6elmtsgeoexo69}{1}{Sur la figure ci-contre, on a
      tracé la droite qui passe par $A$
    et $C$.}&\fa&\vr\\
  \hfill\newline\compo{2}{6elmtsgeoexo69}{1}{Sur la figure ci-contre, les points $A$, $B$ et
    $C$ sont alignés.}&\fa&\vr\\
  \hfill\newline\compo{3}{6elmtsgeoexo69}{1}{En utilisant la figure
    ci-contre, on peut écrire $B\in(AD)$.}&\vr&\fa\\
  \hfill\newline\compo{4}{6elmtsgeoexo69}{1}{Sur la figure ci-contre,
    les droites $(d_1)$ et $(d_2)$ sont perpendiculaires.}&\fa&\vr\\
  \end{VFcor}
\end{center}