exo60.tex

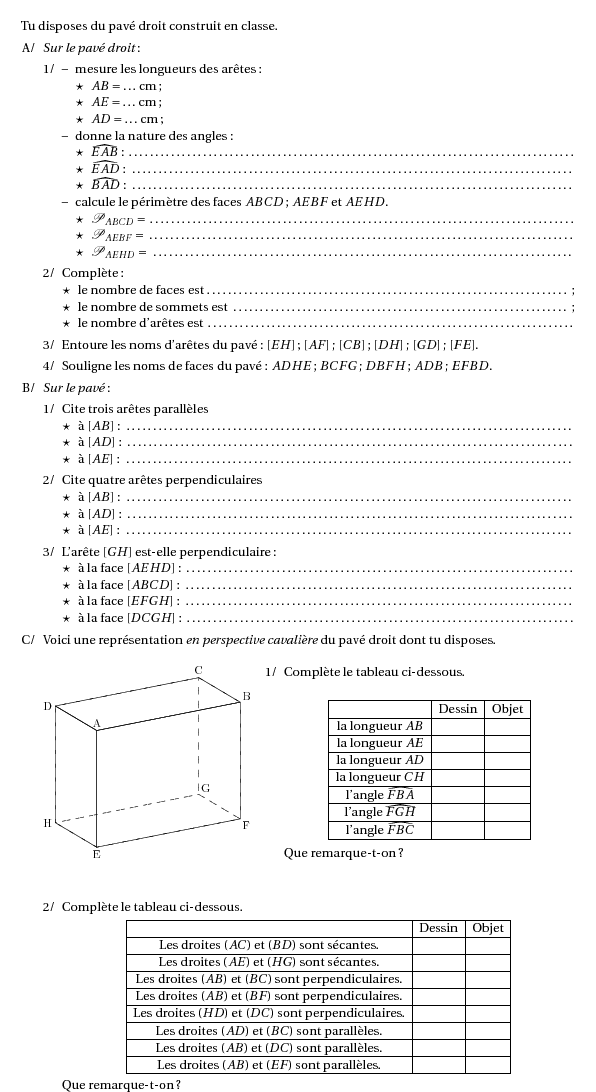
%@metapost:6espaceexo60.mp
Tu disposes du pavé droit construit en classe.
\begin{enumerate}[A/]
\item {\em Sur le pavé droit} :
  \begin{enumerate}[1/]
  \item 
    \begin{itemize}
    \item mesure les longueurs des arêtes :
      \begin{itemize}
      \item[$\star$] $AB=\ldots$~cm;
      \item[$\star$] $AE=\ldots$~cm;
      \item[$\star$] $AD=\ldots$~cm;
      \end{itemize}
    \item donne la nature des angles :
      \begin{itemize}
      \item[$\star$]$\widehat{EAB}$ : \dotfill
      \item[$\star$]$\widehat{EAD}$ : \dotfill
      \item[$\star$]$\widehat{BAD}$ : \dotfill
      \end{itemize}
    \item calcule le périmètre des faces $ABCD$; $AEBF$ et $AEHD$.
      \begin{itemize}
      \item[$\star$] ${\mathscr P}_{ABCD}=$ \dotfill
      \item[$\star$] ${\mathscr P}_{AEBF}=$ \dotfill
      \item[$\star$] ${\mathscr P}_{AEHD}=$ \dotfill
      \end{itemize}
    \end{itemize}
  \item Complète :
    \begin{itemize}
    \item[$\star$] le nombre de faces est\dotfill;
    \item[$\star$] le nombre de sommets est \dotfill;
    \item[$\star$] le nombre d'arêtes est \dotfill
    \end{itemize}
  \item Entoure les noms d'arêtes du pavé : $[EH]$; $[AF]$; $[CB]$; $[DH]$; $[GD]$; $[FE]$.
  \item Souligne les noms de faces du pavé : $ADHE$; $BCFG$; $DBFH$; $ADB$; $EFBD$.
  \end{enumerate}
\item {\em Sur le pavé} :
  \begin{enumerate}[1/]
    \item Cite trois arêtes parallèles
      \begin{itemize}
      \item[$\star$] à $[AB]$ : \dotfill
      \item[$\star$] à $[AD]$ : \dotfill
      \item[$\star$] à $[AE]$ : \dotfill
      \end{itemize}
    \item Cite quatre arêtes perpendiculaires 
      \begin{itemize}
      \item[$\star$] à $[AB]$ : \dotfill
      \item[$\star$] à $[AD]$ : \dotfill
      \item[$\star$] à $[AE]$ : \dotfill
      \end{itemize}
    \item L'arête $[GH]$ est-elle perpendiculaire :
      \begin{itemize}
      \item[$\star$] à la face $[AEHD]$ : \dotfill
      \item[$\star$] à la face $[ABCD]$ : \dotfill
      \item[$\star$] à la face $[EFGH]$ : \dotfill
      \item[$\star$] à la face $[DCGH]$ : \dotfill
      \end{itemize}
  \end{enumerate}
\item Voici une représentation {\em en perspective cavalière} du pavé
  droit dont tu disposes.\par\vspace{5mm}
  \compo{1}{6espaceexo60}{1}{%
    \begin{enumerate}[1/]
    \item Complète le tableau ci-dessous.\\
      \begin{center}
        \begin{tabular}{|c|c|c|}
          \hline
          &Dessin&Objet\\
          \hline
          la longueur $AB$&&\\
          \hline
          la longueur $AE$&&\\
          \hline
          la longueur $AD$&&\\
          \hline
          la longueur $CH$&&\\
          \hline
          l'angle $\widehat{FBA}$&&\\
          \hline
          l'angle $\widehat{FGH}$&&\\
          \hline
          l'angle $\widehat{FBC}$&&\\
          \hline
        \end{tabular}
      \end{center}
      Que remarque-t-on ?
    \end{enumerate}
  }
  \begin{enumerate}[2/]
    %\setcounter{enumi}{1}
  \item Complète le tableau ci-dessous.
    \begin{center}
      \begin{tabular}{|c|c|c|}
        \hline
        &Dessin&Objet\\
        \hline
        Les droites $(AC)$ et $(BD)$ sont sécantes.&&\\
        \hline
        Les droites $(AE)$ et $(HG)$ sont sécantes.&&\\
        \hline
        Les droites $(AB)$ et $(BC)$ sont perpendiculaires.&&\\
        \hline
        Les droites $(AB)$ et $(BF)$ sont perpendiculaires.&&\\
        \hline
        Les droites $(HD)$ et $(DC)$ sont perpendiculaires.&&\\
        \hline
        Les droites $(AD)$ et $(BC)$ sont parallèles.&&\\
        \hline
        Les droites $(AB)$ et $(DC)$ sont parallèles.&&\\
        \hline
        Les droites $(AB)$ et $(EF)$ sont parallèles.&&\\
        \hline
      \end{tabular}
    \end{center}
  Que remarque-t-on ?
  \end{enumerate}
\end{enumerate}