exo14.tex

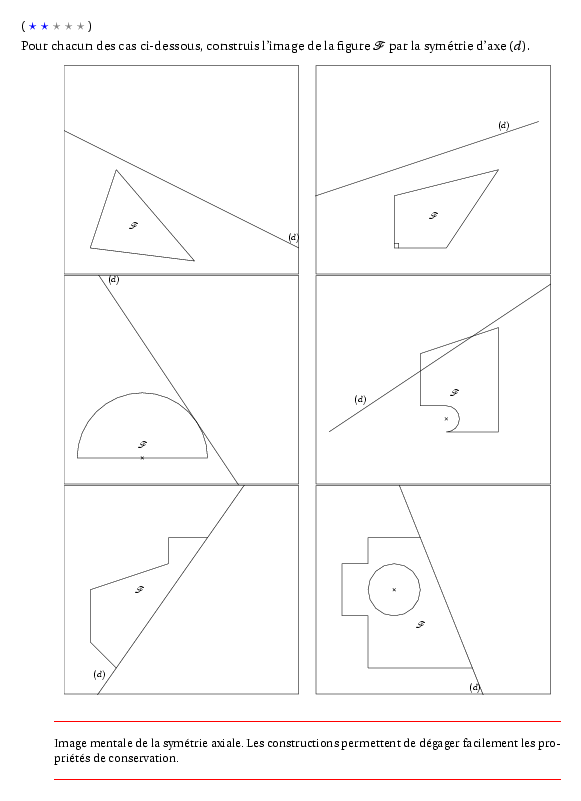
%@P:exocorcp
%@metapost:602symetrieconstruction.mp
%@Dif:2
Pour chacun des cas ci-dessous, construis l'image de la figure $\cal F$ par la symétrie d'axe $(d)$.
\begin{center}
\includegraphics[scale=0.8]{602symetrieconstruction.1}\kern5mm\includegraphics[scale=0.8]{602symetrieconstruction.2}
\\\includegraphics[scale=0.8]{602symetrieconstruction.3}\kern5mm\includegraphics[scale=0.8]{602symetrieconstruction.4}
\\\includegraphics[scale=0.8]{602symetrieconstruction.5}\kern5mm\includegraphics[scale=0.8]{602symetrieconstruction.6}
\end{center}
%@Commentaire: Image mentale de la symétrie axiale. Les constructions permettent de dégager facilement les propriétés de conservation.
%@Correction:
\includegraphics{602symetrieconstruction.7}\kern5mm\includegraphics{602symetrieconstruction.8}
\\\includegraphics{602symetrieconstruction.9}\kern5mm\includegraphics{602symetrieconstruction.10}
\\\includegraphics{602symetrieconstruction.11}\kern5mm\includegraphics{602symetrieconstruction.12}