exo11.tex

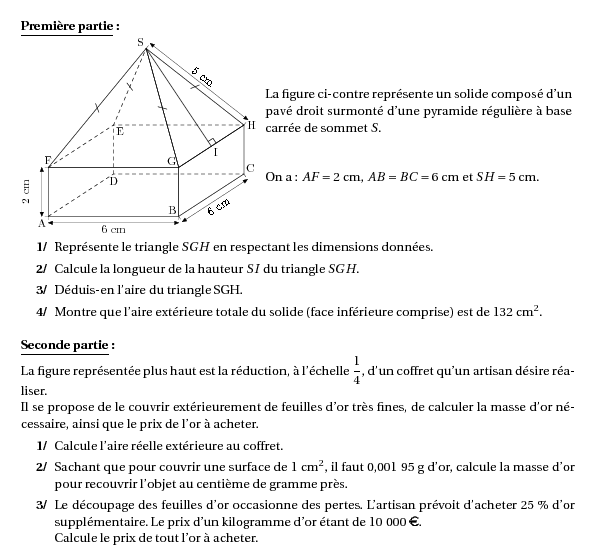
%@metapost:3Problemeexo11.mp
%àAuteur:Véronique Glaçon\par
\textbf{\underline{Première partie} :}
\par\compo{1}{3Problemeexo11}{1}{La figure ci-contre représente un solide composé d'un pavé droit surmonté d'une pyramide régulière à base carrée de sommet $S$. \vspace{1cm}
\\On a : $AF=2$~cm, $AB=BC=6$~cm et $SH=5$~cm.}
 
\begin{myenumerate}
	\item Représente le triangle $SGH$ en respectant les dimensions données.
	\item Calcule la longueur de la hauteur $SI$ du triangle $SGH$.
	\item Déduis-en l'aire du triangle SGH.
	\item Montre que l'aire extérieure totale du solide (face inférieure comprise) est de 132~cm$^2$.
\end{myenumerate}
 
\vspace{0.3cm}
\textbf{\underline{Seconde partie} :}
\\La figure représentée plus haut est la réduction, à l'échelle $\dfrac14$, d'un coffret qu'un artisan désire réaliser. 
\\Il se propose de le couvrir extérieurement de feuilles d'or très fines, de calculer la masse d'or nécessaire, ainsi que le prix de l'or à acheter.
\begin{myenumerate}
	\item Calcule l'aire réelle extérieure au coffret.
	\item Sachant que pour couvrir une surface de $1$~cm$^2$, il faut $\nombre{0,00195}$~g d'or, calcule la masse d'or pour recouvrir l'objet au centième de gramme près.
	\item Le découpage des feuilles d'or occasionne des pertes. L'artisan prévoit d'acheter $25$~\% d'or supplémentaire.
	Le prix d'un kilogramme d'or étant de $\nombre{10000}$~\textgreek{\euro}.
	\\Calcule le prix de tout l'or à acheter.
\end{myenumerate}