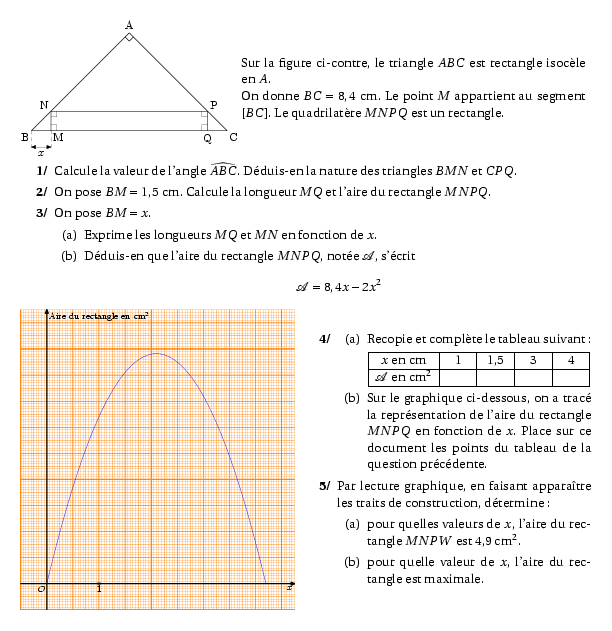
%@metapost: 302dm13.mp %@metapost: 302dm13.1.mp \par\compo{1}{302dm13}{1}{Sur la figure ci-contre, le triangle $ABC$ est rectangle isocèle en $A$.\\On donne $BC=8,4$~cm. Le point $M$ appartient au segment $[BC]$. Le quadrilatère $MNPQ$ est un rectangle. } \begin{myenumerate} \item Calcule la valeur de l'angle $\widehat{ABC}$. Déduis-en la nature des triangles $BMN$ et $CPQ$. \item On pose $BM=1,5$~cm. Calcule la longueur $MQ$ et l'aire du rectangle $MNPQ$. \item On pose $BM=x$. \begin{enumerate} \item Exprime les longueurs $MQ$ et $MN$ en fonction de $x$. \item Déduis-en que l'aire du rectangle $MNPQ$, notée $\cal A$, s'écrit \[{\cal A}=8,4x-2x^2\] \end{enumerate} \end{myenumerate} \par\compo{1}{302dm13.1}{0.8}{ \begin{myenumerate} \setcounter{enumi}{3} \item \begin{enumerate} \item Recopie et complète le tableau suivant : \begin{center} \begin{tabular}{|c|c|c|c|c|} \hline $x$ en cm&1&1,5&3&4\\ \hline $\cal A$ en cm$^2$&\phantom{8,25}&\phantom{8,25}&\phantom{8,25}&\phantom{8,25}\\ \hline \end{tabular} \end{center} \item Sur le graphique ci-dessous, on a tracé la représentation de l'aire du rectangle $MNPQ$ en fonction de $x$. Place sur ce document les points du tableau de la question précédente. \end{enumerate} \item Par lecture graphique, en faisant apparaître les traits de construction, détermine : \begin{enumerate} \item pour quelles valeurs de $x$, l'aire du rectangle $MNPW$ est 4,9~cm$^2$. \item pour quelle valeur de $x$, l'aire du rectangle est maximale. \end{enumerate} \end{myenumerate} }