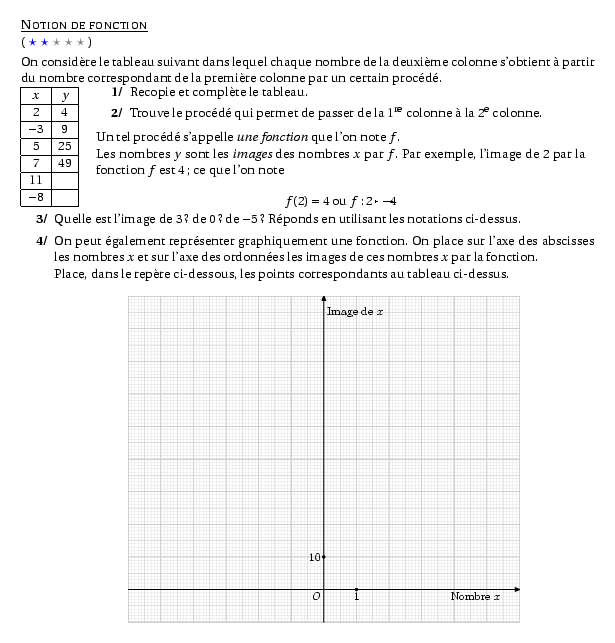
%@Titre: Notion de fonction %@metapost:actiaffine.mp %@Dif:2 On considère le tableau suivant dans lequel chaque nombre de la deuxième colonne s'obtient à partir du nombre correspondant de la première colonne par un certain procédé. \par \dispo{1}{\begin{tabular}{|c|c|} \hline $x$&$y$\\ \hline 2&4\\ \hline $-3$&9\\ \hline 5&25\\ \hline 7&49\\ \hline 11&\\ \hline $-8$&\\ \hline \end{tabular} }{ \begin{myenumerate} \item Recopie et complète le tableau. \item Trouve le procédé qui permet de passer de la 1\iere\ colonne à la 2\ieme\ colonne. \end{myenumerate} Un tel procédé s'appelle {\em une fonction} que l'on note $f$. \\Les nombres $y$ sont les {\em images} des nombres $x$ par $f$. Par exemple, l'image de 2 par la fonction $f$ est 4 ; ce que l'on note \[f(2)=4\mbox{ ou }f:2\mapsto4\] } \begin{myenumerate} \setcounter{enumi}{2} \item Quelle est l'image de 3 ? de 0 ? de $-5$ ? Réponds en utilisant les notations ci-dessus. \item On peut également représenter graphiquement une fonction. On place sur l'axe des abscisses les nombres $x$ et sur l'axe des ordonnées les images de ces nombres $x$ par la fonction. \\Place, dans le repère ci-dessous, les points correspondants au tableau ci-dessus. \[\includegraphics{actiaffine.3}\] \end{myenumerate}