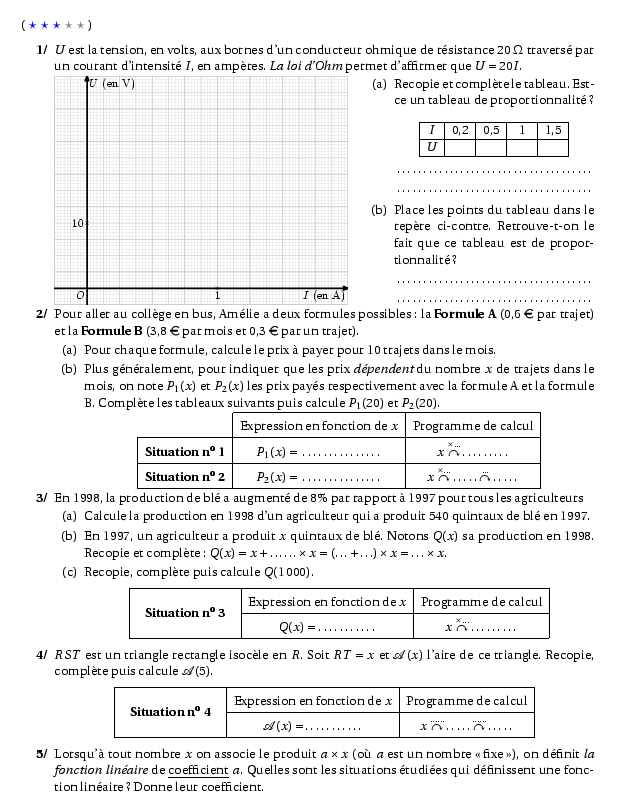
%@metapost:303an6act1.mp %@Dif:3 \begin{myenumerate} \item $U$ est la tension, en volts, aux bornes d'un conducteur ohmique de résistance $20~\Omega$ traversé par un courant d'intensité $I$, en ampères. {\em La loi d'Ohm} permet d'affirmer que $U=20I$. \par\compo{1}{303an6act1}{1}{\begin{enumerate} \item Recopie et complète le tableau. Est-ce un tableau de proportionnalité ? \[ \begin{tabular}{|c|c|c|c|c|} \hline $I$&0,2&0,5&1&1,5\\ \hline $U$&\phantom{0,2}&\phantom{0,2}&\phantom{0,2}&\phantom{0,2}\\ \hline \end{tabular} \] \dotfill\par \par\dotfill\par \item Place les points du tableau dans le repère ci-contre. Retrouve-t-on le fait que ce tableau est de proportionnalité ? \par\dotfill\par \par\dotfill\par \end{enumerate} } \item Pour aller au collège en bus, Amélie a deux formules possibles : la {\bf Formule A} (0,6~\textgreek{\euro} par trajet) et la {\bf Formule B} (3,8~\textgreek{\euro} par mois et 0,3~\textgreek{\euro} par un trajet). \begin{enumerate} \item Pour chaque formule, calcule le prix à payer pour 10 trajets dans le mois. \item Plus généralement, pour indiquer que les prix {\em dépendent} du nombre $x$ de trajets dans le mois, on note $P_1(x)$ et $P_2(x)$ les prix payés respectivement avec la formule A et la formule B. Complète les tableaux suivants puis calcule $P_1(20)$ et $P_2(20)$. \renewcommand{\arraystretch}{1.5} \begin{center} \begin{tabular}{|c|c|c|} \cline{2-3} \multicolumn{1}{c|}{}&Expression en fonction de $x$&Programme de calcul\\ \hline {\bf Situation \no1}&$P_1(x)=\hbox to2.5cm{\dotfill}$&$x\stackrel{\times\ldots}{\curvearrowright}\dotfill$\\ \hline {\bf Situation \no2}&$P_2(x)=\hbox to2.5cm{\dotfill}$&$x\stackrel{\times\ldots}{\curvearrowright}\dotfill\stackrel{\ldots}{\curvearrowright}\dotfill$\\ \hline \end{tabular} \end{center} \renewcommand{\arraystretch}{1} \end{enumerate} \item En 1998, la production de blé a augmenté de 8\% par rapport à 1997 pour tous les agriculteurs \begin{enumerate} \item Calcule la production en 1998 d'un agriculteur qui a produit 540 quintaux de blé en 1997. \item En 1997, un agriculteur a produit $x$ quintaux de blé. Notons $Q(x)$ sa production en 1998. Recopie et complète : $Q(x)=x+\ldots\ldots\times x=\left(\ldots+\ldots\right)\times x=\ldots\times x$. \item Recopie, complète puis calcule $Q(1\,000)$. \renewcommand{\arraystretch}{1.5} \[\begin{tabular}{|c|c|c|} \hline \multirow{2}{3cm}{\centerline{\bf Situation \no3}}&Expression en fonction de $x$&Programme de calcul\\ \cline{2-3} &$Q(x)=\dotfill$&$x\stackrel{\times\ldots}{\curvearrowright}\dotfill$\\ \hline \end{tabular} \] \renewcommand{\arraystretch}{1} \end{enumerate} \item $RST$ est un triangle rectangle isocèle en $R$. Soit $RT=x$ et ${\cal A}(x)$ l'aire de ce triangle. Recopie, complète puis calcule ${\cal A}(5)$. \renewcommand{\arraystretch}{1.5} \[\begin{tabular}{|c|c|c|} \hline \multirow{2}{3cm}{\centerline{\bf Situation \no4}}&Expression en fonction de $x$&Programme de calcul\\ \cline{2-3} &${\cal A}(x)=\dotfill$&$x\stackrel{\ldots\ldots}{\curvearrowright}\dotfill\stackrel{\ldots\ldots}{\curvearrowright}\dotfill$\\ \hline \end{tabular} \] \renewcommand{\arraystretch}{1} \item Lorsqu'à tout nombre $x$ on associe le produit $a\times x$ (où $a$ est un nombre \og{}fixe\fg{}), on définit {\em la fonction linéaire} de \underline{coefficient} $a$. Quelles sont les situations étudiées qui définissent une fonction linéaire ? Donne leur coefficient. \end{myenumerate}