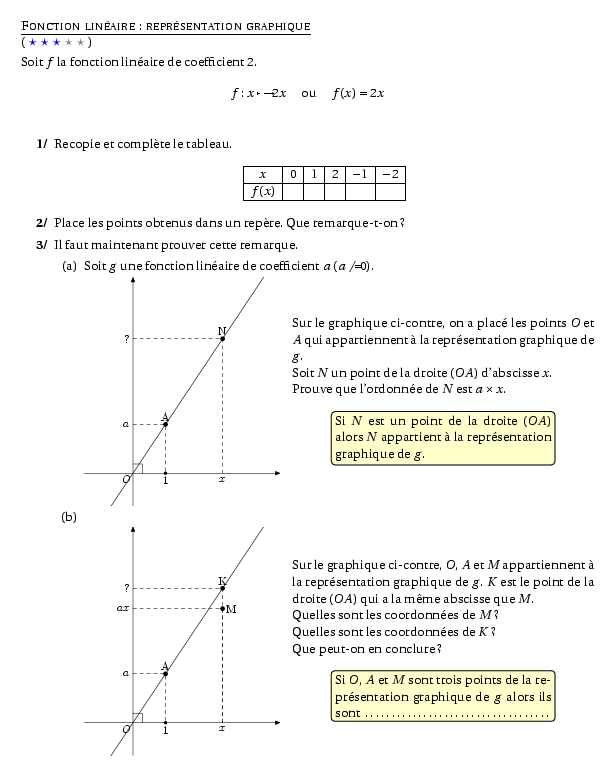
%@metapost:actiaffine.mp %@Titre: Fonction linéaire : représentation graphique %@Dif:3 Soit $f$ la fonction linéaire de coefficient 2. \[f:x\mapsto2x\quad\mbox{ ou }\quad f(x)=2x\] \begin{myenumerate} \item Recopie et complète le tableau. \[\begin{tabular}{|c|c|c|c|c|c|} \hline $x$&0&1&2&$-1$&$-2$\\ \hline $f(x)$&&&&&\\ \hline \end{tabular} \] \item Place les points obtenus dans un repère. Que remarque-t-on ? \item Il faut maintenant prouver cette remarque. \begin{enumerate} \item Soit $g$ une fonction linéaire de coefficient $a$ ($a\not=0$). \par\compo{1}{actiaffine}{1}{Sur le graphique ci-contre, on a placé les points $O$ et $A$ qui appartiennent à la représentation graphique de $g$. \\Soit $N$ un point de la droite $(OA)$ d'abscisse $x$. \\Prouve que l'ordonnée de $N$ est $a\times x$. \[\encadrecouleur{fond1}{Si $N$ est un point de la droite $(OA)$ alors $N$ appartient à la représentation graphique de $g$.}\] } \item\subitem{} \par\compo{2}{actiaffine}{1}{Sur le graphique ci-contre, $O$, $A$ et $M$ appartiennent à la représentation graphique de $g$. $K$ est le point de la droite $(OA)$ qui a la même abscisse que $M$. \\Quelles sont les coordonnées de $M$ ? \\Quelles sont les coordonnées de $K$ ? \\Que peut-on en conclure ? \[\encadrecouleur{fond1}{Si $O$, $A$ et $M$ sont trois points de la représentation graphique de $g$ alors ils sont \dotfill}\] } \end{enumerate} \end{myenumerate}