exo36.tex

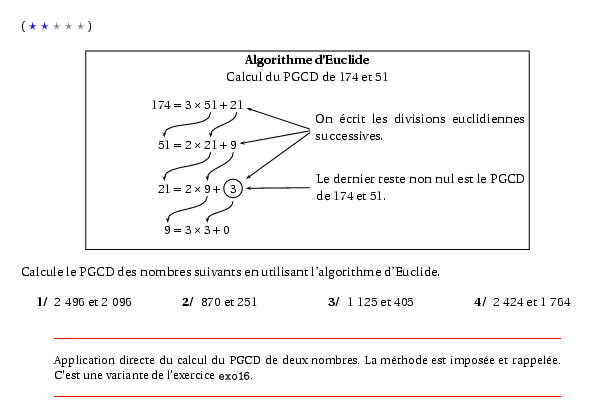
%@P:exocorcp
%@Dif:2
\begin{center}
  \psframebox{
    \begin{minipage}{0.75\linewidth}
      \centerline{\textbf{Algorithme d'Euclide}}
      \par\centerline{Calcul du PGCD de 174 et 51}\par
      \begin{multicols}{2}
        \[\Eqalign{
          174&=3\times\rnode{A1}{51}+\rnode{B1}{21}\cr
          \cr
          \rnode{D1}{51}&=2\times\rnode{A2}{21}+\rnode{B2}{9}\cr
          \cr
          \rnode{D2}{21}&=2\times\rnode{A3}{9}+\rnode{B3}{\pscirclebox{3}}\cr
          \cr
          \rnode{D3}{9}&=3\times\rnode{A4}{3}+0\cr
          }\]
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{A1}{D1}
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{B1}{A2}
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{A2}{D2}
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{B2}{A3}
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{A3}{D3}
          \nccurve[nodesep=1mm,angleA=-90,angleB=90]{->}{B3}{A4}
          \par\columnbreak\par\vspace*{5mm}\par\rnode{E1}{}
            \begin{minipage}{1.0\linewidth}
              On écrit les divisions euclidiennes successives.
            \end{minipage}
            %}
            \par\vspace{1cm}\par
            \rnode{E2}{
            \begin{minipage}{1.0\linewidth}
              Le dernier reste non nul est le PGCD de 174 et 51.
            \end{minipage}
            }
            \ncline[nodesep=1mm]{->}{E1}{B1}\ncline[nodesep=1mm]{->}{E1}{B2}\ncline[nodesep=1mm]{->}{E1}{B3}\ncline[nodesep=1mm]{->}{E2}{B3}
      \end{multicols}
    \end{minipage}
}
\end{center}
Calcule le PGCD des nombres suivants en utilisant l'algorithme d'Euclide.
\begin{multicols}{4}
\begin{myenumerate}
  \item \nombre{2496} et \nombre{2096}
  \item 870 et 251
  \item \nombre{1125} et 405
  \item \nombre{2424} et \nombre{1764}
\end{myenumerate}
\end{multicols}
%@Correction:
\begin{multicols}{2}
\begin{myenumerate}
  \item\subitem{}\par \begin{center}
\begin{tabular}{cccl}
$a$&$b$&$r$&car\ldots\\
\hline
2\,496&2\,096&400&$2\,496=2\,096\times1+400$\\
2\,096&400&96&$2096=400\times5+96$\\
400&96&16&$400=96\times4+16$\\
96&16&0&$96=16\times6+0$\\
\end{tabular}
\end{center}
\par Le $\pgcd(2\,496;2\,096)$ est 16.
\item\subitem{}\par \begin{center}
\begin{tabular}{cccl}
$a$&$b$&$r$&car\ldots\\
\hline
870&251&117&$870=251\times3+117$\\
251&117&17&$251=117\times2+17$\\
117&17&15&$117=17\times6+15$\\
17&15&2&$17=15\times1+2$\\
15&2&1&$15=2\times7+1$\\
2&1&0&$2=1\times2+0$\\
\end{tabular}
\end{center}
\par Le $\pgcd(870;251)$ est 1.
\item\subitem{}\par \begin{center}
\begin{tabular}{cccl}
$a$&$b$&$r$&car\ldots\\
\hline
1\,125&405&315&$1\,125=405\times2+315$\\
405&315&90&$405=315\times1+90$\\
315&90&45&$315=90\times3+45$\\
90&45&0&$90=45\times2+0$\\
\end{tabular}
\end{center}
\par Le $\pgcd(1\,125;405)$ est 45.
\item\subitem{}\par \begin{center}
\begin{tabular}{cccl}
$a$&$b$&$r$&car\ldots\\
\hline
2\,424&1\,764&660&$2\,424=1\,764\times1+660$\\
1\,764&660&444&$1\,764=660\times2+444$\\
660&444&216&$660=444\times1+216$\\
444&216&12&$444=216\times2+12$\\
216&12&0&$216=12\times18+0$\\
\end{tabular}
\end{center}
\par Le $\pgcd(2\,424;1\,764)$ est 12.
\end{myenumerate}
\end{multicols}
%@Commentaire: Application directe du calcul du PGCD de deux nombres. La méthode est imposée et rappelée. C'est une variante de l'exercice \verb+exo16+.